题目内容
5.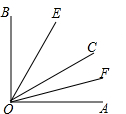 如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.(1)若∠AOB=90°,∠AOC=40°,求∠EOF的度数;
(2)若∠AOB=a,求∠EOF的度数.
分析 (1)首先求得∠BOC,然后根据角的平分线的定义求得∠EOC和∠COF,然后根据∠EOF=∠EOC+∠COF求解;
(2)根据角的平分线的定义求得∠EOC=$\frac{1}{2}$∠BOC,∠COF=$\frac{1}{2}$∠AOC,然后根据∠EOF=∠EOC+∠COF=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠COF=$\frac{1}{2}$(∠BOC+∠AOC)即可求解.
解答 解:(1)∠BOC=∠AOB-∠AOC=90°-40°=50°,
∵OE平分∠BOC,OF平分∠AOC,
∴∠EOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×50°=25°,∠COF=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×40°=20°,
∴∠EOF=∠EOC+∠COF=25°+20°=45°;
(2)∵OE平分∠BOC,OF平分∠AOC,
∴∠EOC=$\frac{1}{2}$∠BOC,∠COF=$\frac{1}{2}$∠AOC,
∴∠EOF=∠EOC+∠COF=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠COF=$\frac{1}{2}$(∠BOC+∠AOC)=$\frac{1}{2}$∠AOB=$\frac{1}{2}$α.
点评 本题考查了角的平分线的定义,根据角的平分线的定义以及角的和差关系得到∠EOF=∠EOC+∠COF=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠COF=$\frac{1}{2}$(∠BOC+∠AOC)=$\frac{1}{2}$∠AOB是关键.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 彩票中奖的概率是1%,则买100张彩票一定会中奖 | |
| B. | 一组数据的中位数就是这组数据正中间的数 | |
| C. | 鞋店老板进货时最关心的是鞋码的众数 | |
| D. | 甲每次考试成绩都比乙好,则方差S甲2<S乙2 |
15.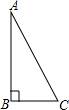 在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:
在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:
小孟说:“他们的作法都错误.”你的观点是( )
 在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:
在一次数学课上,张老师布置了一项作业:以Rt△ABC(如图所示)的两直角边AB,BC为邻边作矩形ABCD,下面是小钟和小国各自的作法:| 小钟作法: (1)作AC的垂直平分线MN,垂足为点O; (2)连接BO,并延长BO至点D,使DO=BO; (3)连接AD,CD 所以,四边形ABCD就是所要求作的矩形 |
| 小国作法: (1)分别以A,C为圆心,以BC,AB为半径作弧,两弧交于点D; (2)连接AD,CD. 所以,四边形ABCD就是所要求作的矩形. |
| A. | 小钟的作法正确 | B. | 小国的作法正确 | ||
| C. | 小钟和小国的作法都正确 | D. | 赞同小孟的观点 |
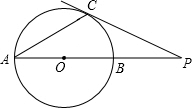 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则BP的长为$\sqrt{3}$.
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则BP的长为$\sqrt{3}$.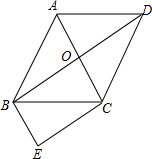 如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.
如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.
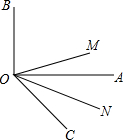 如图,ON平分∠AOC,OM平分∠BOC.
如图,ON平分∠AOC,OM平分∠BOC.