题目内容
7. 如图,两条直线表示函数y1=k1x与y2=k2x+b的图象,根据图象回答:
如图,两条直线表示函数y1=k1x与y2=k2x+b的图象,根据图象回答:(1)直线AB表示y2=k2x+b的图象,直线OB表示y1=k1x的图象.
(2)随着x的增大,y1增大,y2增大.
(3)当x>0时,y1>0,y2>0.
(4)当x=$\frac{1}{2}$时,y1和y2哪个大?说明理由.
(5)当x满足什么条件时,y1总大于y2?
分析 (1)根据直线OB表示正比例函数,而直线AB表示一般的一次函数进行判断即可;
(2)根据函数图象从左往右上升,即可得到函数的增减性;
(3)根据第一象限内函数图象在x轴的上方,即可得到结论;
(4)根据当x=$\frac{1}{2}$时,在函数图象上的对应点的位置,即可得到结论;
(5)根据函数图象交点两侧部分的函数图象的上下位置关系进行判断.
解答 解:(1)由图可得,直线AB表示y2=k2x+b的图象,直线OB表示y1=k1x的图象.
故答案为:y2=k2x+b,y1=k1x;
(2)由图可得,随着x的增大,y1增大,y2增大.
故答案为:增大,增大;
(3)由图可得,当x>0时,y1>0,y2>0.
故答案为:>,>;
(4)由图可得,当x=$\frac{1}{2}$时,y1<y2,
理由:当x=$\frac{1}{2}$时,在函数y2=k2x+b的图象上对应的点在上方,在函数y1=k1x的图象上对应的点在下方,
故存在y1<y2;
(5)由图可得,当x>2时,函数y2=k2x+b的图象在函数y1=k1x的图象的下方,
故当x>2时,y1总大于y2.
点评 本题主要考查了一次函数与一元一次不等式的关系,从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
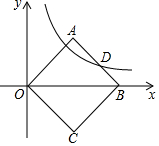 如图,已知正方形OABC的一个顶点在原点,且对角线OB在x轴的正半轴上,反比例函数y=$\frac{k}{x}$在第一象限内的图象与AB边交于点D,若OA2-AD2=8,求反比例函数的解析式.
如图,已知正方形OABC的一个顶点在原点,且对角线OB在x轴的正半轴上,反比例函数y=$\frac{k}{x}$在第一象限内的图象与AB边交于点D,若OA2-AD2=8,求反比例函数的解析式.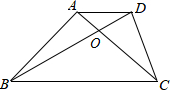 如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠BOC=105度.
如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠BOC=105度.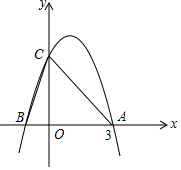 如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.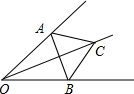 如图所示,OA=OB,AC=BC,求证:OC⊥AB.
如图所示,OA=OB,AC=BC,求证:OC⊥AB.