题目内容
2. 如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠BOC=105度.
如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠BOC=105度.
分析 作AF⊥BC于F,DE⊥BC于E,根据等腰直角三角形的性质用AB表示出BC及AF的长,由锐角三角函数的定义求出∠1的度数,根据BC三角形内角和等于180°得出∠BOC的度数即可.
解答 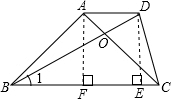 解:如图,作AF⊥BC于F,DE⊥BC于E,
解:如图,作AF⊥BC于F,DE⊥BC于E,
在Rt△ABC中,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴BC=$\sqrt{2}$AB,AF=$\frac{\sqrt{2}}{2}$AB,
∴AF=$\frac{1}{2}$BC.
又∵DE=AF,
∴DE=$\frac{1}{2}$BC=$\frac{1}{2}$BD,
∴$\frac{DE}{BD}$=$\frac{1}{2}$,
∴sin∠1=$\frac{1}{2}$,
∴∠1=30°,
∴∠BOC=180°-30°-45°=105°.
故答案为:105.
点评 本题考查了梯形及等腰三角形的判定,难度一般,关键是巧妙作辅助线进行解答.

练习册系列答案
相关题目
12.当a=1,b=-2时,代数式2a2-ab的值是( )
| A. | -4 | B. | 0 | C. | 4 | D. | 7 |
 如图,两条直线表示函数y1=k1x与y2=k2x+b的图象,根据图象回答:
如图,两条直线表示函数y1=k1x与y2=k2x+b的图象,根据图象回答: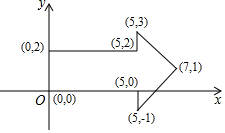 如图,箭头图案是将坐标分别为(0,0),(0,2),(5,2),(5,3),(7,1),(5,-1),(5,0),(0,0)的点用线段依次连接而成的,现把图中的格点分别如下变换:
如图,箭头图案是将坐标分别为(0,0),(0,2),(5,2),(5,3),(7,1),(5,-1),(5,0),(0,0)的点用线段依次连接而成的,现把图中的格点分别如下变换: