题目内容
12.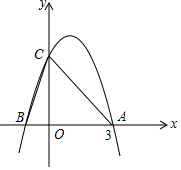 如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.(1)求m的值;
(2)求直线AC的解析式;
(3)求△ABC的面积.
分析 (1)把A点坐标代入抛物线解析式可确定m的值;
(2)先通过抛物线解析式确定C点坐标,然后利用待定系数法求直线AC的解析式;
(3)先通过解方程-x2+2x+3=0确定B点坐标,然后根据三角形面积公式求解.
解答 解:(1)把A(3,0)代入y=-x2+2x+m得-9+6+m=0,
解得m=3;
(2)抛物线解析式为y=-x2+2x+3,
当x=0时,y=-x2+2x+3=3,则C(0,3);
设直线AC的解析式为y=kx+b,
根据题意得$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
所以直线AC的解析式为y=-x+3;
(3)当y=0时,-x2+2x+3=0,解得x1=3,x2=-1,则B(-1,0),
所以△ABC的面积=$\frac{1}{2}$×(3+1)×3=6.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程的问题.也考查了待定系数法法求与一次函数解析式.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

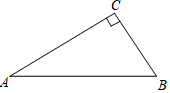 折叠如图所示的直角三角形纸片ABC,使点C落在AB上的点E处,折痕为AD(点D在BC边上),用直尺和圆规画出折痕AD.(保留作图痕迹,不写作法).
折叠如图所示的直角三角形纸片ABC,使点C落在AB上的点E处,折痕为AD(点D在BC边上),用直尺和圆规画出折痕AD.(保留作图痕迹,不写作法).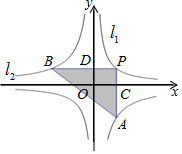 如图,两个反比例函数$y=\frac{k}{x}$和y=-$\frac{2}{x}$的图象分别是l1和l2,E(2,$\frac{1}{2}$)是l1上的一点.
如图,两个反比例函数$y=\frac{k}{x}$和y=-$\frac{2}{x}$的图象分别是l1和l2,E(2,$\frac{1}{2}$)是l1上的一点. 如图,两条直线表示函数y1=k1x与y2=k2x+b的图象,根据图象回答:
如图,两条直线表示函数y1=k1x与y2=k2x+b的图象,根据图象回答: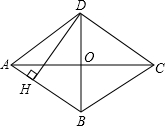 如图所示,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB 于点H,且DH与AC交于点G,则AH的长是多少?
如图所示,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB 于点H,且DH与AC交于点G,则AH的长是多少?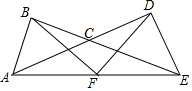 如图,两个等腰直角三角形ABC、CDE,顶点C重合,点B、C、E共线,F是AE的中点,连BF、DF,求证:BF=DF且BF⊥DF.
如图,两个等腰直角三角形ABC、CDE,顶点C重合,点B、C、E共线,F是AE的中点,连BF、DF,求证:BF=DF且BF⊥DF.