题目内容
18.在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△AOB全等,则C点的坐标为(2,4)或(-2,0)或(-2,4).分析 根据全等三角形的判定和已知点的坐标画出图形,即可得出答案.
解答 解:如图所示:
有三个点符合,
∵点A(2,0),B(0,4),
∴OB=4,OA=2,
∵△BOC与△AOB全等,
∴OB=OB=4,OA=OC=2,
∴C1(-2,0),C2(-2,4),C3(2,4).
故答案为:(2,4)或(-2,0)或(-2,4).
点评 本题考查了全等三角形的判定定理,点的坐标的应用,能求出符合条件的所有情况是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
相关题目
8.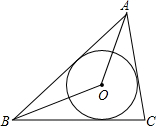 如图,⊙O是△ABC的内切圆,若∠AOB=120°,则∠ACB的度数是( )
如图,⊙O是△ABC的内切圆,若∠AOB=120°,则∠ACB的度数是( )
 如图,⊙O是△ABC的内切圆,若∠AOB=120°,则∠ACB的度数是( )
如图,⊙O是△ABC的内切圆,若∠AOB=120°,则∠ACB的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
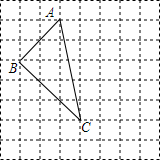 在如图所示的正方形网格中,格点三角形ABC(即顶点都是网格线的交点)的顶点A、C的坐标为A(-1,4)、B(-3,2).
在如图所示的正方形网格中,格点三角形ABC(即顶点都是网格线的交点)的顶点A、C的坐标为A(-1,4)、B(-3,2).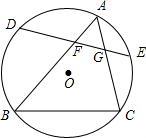 如图,△ABC三个顶点都在⊙O上,D,E分别为$\widehat{AB}$,$\widehat{AC}$中点,弦DE交AB于点F,交AC于点G,求证:AF•AG=DF•EG.
如图,△ABC三个顶点都在⊙O上,D,E分别为$\widehat{AB}$,$\widehat{AC}$中点,弦DE交AB于点F,交AC于点G,求证:AF•AG=DF•EG.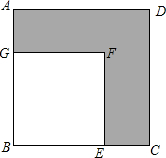 如图,工人张师傅要在一块大正方形ABCD中切下一块小的正方形BEFG,若阴影部分面积为240mm2,AB=2x+8,BE=2x-4,求大正方形的边长.
如图,工人张师傅要在一块大正方形ABCD中切下一块小的正方形BEFG,若阴影部分面积为240mm2,AB=2x+8,BE=2x-4,求大正方形的边长.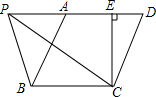 如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;
如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;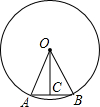 如图,⊙O的半径为20,$\widehat{AB}$的度数为36°,求弦AB及其弦心距OC的长(精确到0.1).
如图,⊙O的半径为20,$\widehat{AB}$的度数为36°,求弦AB及其弦心距OC的长(精确到0.1).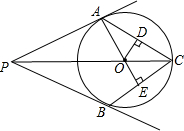 从⊙O外一点P引⊙O的切线PA、PB,切点分别为A、B两点,连结PO并延长PO交⊙O于点C,连接CA,CB,OD⊥AC,OE⊥CB,垂足分别为D、E,求证:OD=OE.
从⊙O外一点P引⊙O的切线PA、PB,切点分别为A、B两点,连结PO并延长PO交⊙O于点C,连接CA,CB,OD⊥AC,OE⊥CB,垂足分别为D、E,求证:OD=OE.