题目内容
1.已知菱形ABCD,点A和点D分别在x轴的负半轴和y轴的正半轴上,0为坐标轴原点,点A,D坐标分别是A(-4,0)和D(0,3),抛物线的对称轴是直线x=$\frac{5}{2}$;抛物线的图象y=ax2+bx+c(a≠0)经过点B,D;
(1)求出抛物线对应的解析式.
(2)试判断C点是否在抛物线上,并说明理由.
(3)图(1)中,若M点在CB所在直线下方,过点M作MN∥OD,交BC于点N;设点M的横坐标为a,MN的长度为b,并求出b最值.
(4)图(2)中,在(3)的条件下,设线段MN与x轴的交点为E,过点C作CF⊥OX,垂足是F,当△BEN与△BCF相似比为1:2时,连接MF;试判断四边形NMFC是否为平行四边形,并求出此时点E的坐标.
分析 (1))由抛物线与x轴的交点B(1,0),且抛物线的对称轴为x=$\frac{5}{2}$,推出抛物线与x轴的另一个交点为(4,0),设抛物线解析式为y=a(x-1)(x-4),将点D(0,3)代入,得:4a=3,由此即可解决问题.
(2)求出点C坐标,利用待定系数法即可判定.
(3)求出直线BC的解析式,由MN∥OD,点M的横坐标为a,可得M(a,$\frac{3}{4}$a2-$\frac{15}{4}$a+3)、N(a,$\frac{3}{4}$a-$\frac{3}{4}$),当点M在在CB所在直线下方时,MN=($\frac{3}{4}$a-$\frac{3}{4}$)-($\frac{3}{4}$a2_$\frac{15}{4}$a+3)=-$\frac{3}{4}$a2+$\frac{9}{2}$a-$\frac{15}{4}$=-$\frac{3}{4}$(a-3)2+$\frac{11}{2}$,利用二次函数的性质即可解决问题.
(4)结论:四边形MNCF是平行四边形.由△BEN与△BCF相似比为1:2,推出NE:FC=BE+BF=1:2,推出BE=EF=2,由F(5,0),B(1,0),推出E(3,0),推出N(3,$\frac{3}{2}$),M(3,-$\frac{3}{2}$),可得MN=3,由此即可证明.
解答 解:(1)∵抛物线与x轴的交点B(1,0),且抛物线的对称轴为x=$\frac{5}{2}$,
∴抛物线与x轴的另一个交点为(4,0),
设抛物线解析式为y=a(x-1)(x-4),
将点D(0,3)代入,得:4a=3,
解得:a=$\frac{3}{4}$,
∴抛物线解析式为y=$\frac{3}{4}$(x-1)(x-4)=$\frac{3}{4}$x2-$\frac{15}{4}$x+3;
(2)∵OA=4,OD=3,
∴AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=5,
∵四边形ABCD是菱形,
∴AB∥CD,且AB=CD=AD=5,
则点C坐标为(5,3),
当x=5时,y=$\frac{3}{4}$×25-$\frac{15}{4}$×5+3=3,
∴点C在抛物线上;
(3)设直线BC解析式为y=kx+b,
将点B(1,0)、C(5,3)代入,得:$\left\{\begin{array}{l}{k+b=0}\\{5k+b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-\frac{3}{4}}\end{array}\right.$,
∴直线BC解析式为y=$\frac{3}{4}$x-$\frac{3}{4}$;
∵MN∥OD,点M的横坐标为a,
∴M(a,$\frac{3}{4}$a2-$\frac{15}{4}$a+3)、N(a,$\frac{3}{4}$a-$\frac{3}{4}$),
当点M在在CB所在直线下方时,MN=($\frac{3}{4}$a-$\frac{3}{4}$)-($\frac{3}{4}$a2_$\frac{15}{4}$a+3)=-$\frac{3}{4}$a2+$\frac{9}{2}$a-$\frac{15}{4}$=-$\frac{3}{4}$(a-3)2+$\frac{11}{2}$,
∵-$\frac{3}{4}$<0,
∴a=3时,MN有最大值,最大值为$\frac{11}{2}$,
∴b的最大值为$\frac{11}{2}$.
(4)结论:四边形MNCF是平行四边形.
理由:∵△BEN与△BCF相似比为1:2,
∴NE:FC=BE+BF=1:2,
∴BE=EF=2,
∵F(5,0),B(1,0),
∴E(3,0),
∴N(3,$\frac{3}{2}$),M(3,-$\frac{3}{2}$),
∴MN=3,
∵CF=3,
∴MN∥CF,MN=CF,
∴四边形MNCF是平行四边形,此时E(3,0).
点评 本题考查二次函数综合题、待定系数法、勾股定理、一次函数的应用、平行四边形的性质和判定、相似三角形的性质等知识,解题的关键是学会构建二次函数解决最值问题,学会用方程的思想思考问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | m2-(2m-n-p)=m2-2m+n+p | B. | m-n+p-q=m-(n+q-p) | ||
| C. | 3m-5n-1+2p=-(-3m)-[5n-(2p-1)] | D. | m+1-(-n+p)=-(-1+n-m+p) |
| A. | b>0 | B. | b-a<0 | C. | b-a>0 | D. | a+b>0 |
| A. | 为了审核书稿中的错别字,选择抽样调查 | |
| B. | 为了了解春节联欢晚会的收视率,选择普查 | |
| C. | “经过由交通信号灯的路口,遇到红灯”是必然事件 | |
| D. | “射击运动员射击一次,命中靶心”是随机事件 |
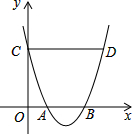 如图,抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,与抛物线交于点D,若OA=1,CD=4,则线段AB的长为( )
如图,抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,过点C作CD∥x轴,与抛物线交于点D,若OA=1,CD=4,则线段AB的长为( ) 把四张形状大小完全相同的小长方形卡片(如图①),卡片长为x,宽为y,不重叠地放在一个底面为长方形(宽为a)的盒子底部(如图②),盒底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分周长和是4b(用只含b的代数式表示).
把四张形状大小完全相同的小长方形卡片(如图①),卡片长为x,宽为y,不重叠地放在一个底面为长方形(宽为a)的盒子底部(如图②),盒底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分周长和是4b(用只含b的代数式表示). 如图,在△ABC中,∠ABC=45°,AD、BE是△ABC的高,AD、BE相交于点F.
如图,在△ABC中,∠ABC=45°,AD、BE是△ABC的高,AD、BE相交于点F.