题目内容
13. 如图,在△ABC中,∠ABC=45°,AD、BE是△ABC的高,AD、BE相交于点F.
如图,在△ABC中,∠ABC=45°,AD、BE是△ABC的高,AD、BE相交于点F.求证:BF=AC.
分析 要证明BF=AC,只要证明△BDF≌△ADC即可,根据题目中的条件可以找到两个三角形全等的条件,从而可以解答本题.
解答 证明:∵AD、BE为△ABC的高,
∴∠ADB=∠ADC=∠BEC=90°,
∴∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
∵∠ABC=45°,∠ADB=90°,
∴∠DAB=45°,
∴∠ABD=∠BAD,
∴AD=BD,
在△BDF和△ADC中,
$\left\{\begin{array}{l}{∠DBF=∠DAC}\\{BD=AD}\\{∠BDF=∠ADC}\end{array}\right.$,
∴△BDF≌△ADC(ASA),
∴BF=AC.
点评 本题考查全等三角形的判定与性质,解答本题的关键是明确题意,找出所要证明结论需要的条件,利用三角形全等的知识解答.

练习册系列答案
相关题目
8. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2018个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2018个点的横坐标为( )
 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2018个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2018个点的横坐标为( )| A. | 44 | B. | 45 | C. | 46 | D. | 47 |
5.下列方程组是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x-y=1}\\{xy=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{1}{x}-1=y}\\{3x+y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{{x}^{2}-x-2=0}\\{y=x+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{4x-y=-1}\\{y=2x+3}\end{array}\right.$ |
3.下列各式利用完全平方公式计算正确的是( )
| A. | (x+3)2=x2+9 | B. | (-2a+b)2=4a2+4ab+b2 | ||
| C. | (a-2b)2=a2-2ab+4b2 | D. | ($\frac{1}{2}$-x)2=x2-x+$\frac{1}{4}$ |
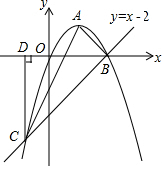 如图,已知抛物线y=-x2+2x的顶点为A,直线y=x-2与抛物线交于B,C两点.
如图,已知抛物线y=-x2+2x的顶点为A,直线y=x-2与抛物线交于B,C两点.