题目内容
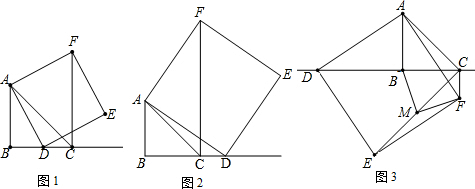
5.如图1所示,在Rt△ABC中,∠ACB=90°,点D为边BC上任意一点,以直线AD为对称轴,作Rt△ABC的轴对称图形Rt△AEF,点M、点N、点P、点Q分别为AB、BC、EF、EA的中点.(1)求证:MN=PQ;
(2)如图2,当BD=$\frac{1}{3}BC$时,判断点M、点N、点P、点Q围成的四边形的形状,并说明理由;
(3)若BC=6,请你直接写出点M、点N、点P、点Q围成的图形共有哪些形状及对应的BD的取值范围.
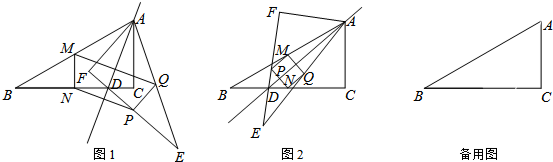
分析 (1)根据三角形中位线定理证明MN=$\frac{1}{2}$AC,PQ=$\frac{1}{2}$AF,根据轴对称得到AC=AF,得到答案;
(2)根据相似三角形的判定定理证明△PDN∽△EDB,得到MQ∥PN且MQ=PN,得到四边形MQNP是平行四边形,根据MN=PQ,证明四边形MQNP是矩形;
(3)由(1)(2)的结论进行解答即可.
解答 (1)证明:如图1,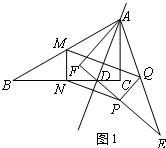
∵△ABC与△AEF关于直线AD对称,
∴△ABC≌△AEF,
∴AC=AF,
∵点M、N、P、Q分别是AB、BC、EF、EA的中点,
∴MN、PQ分别是△ABC和△AEF的中位线,
∴MN=$\frac{1}{2}$AC,PQ=$\frac{1}{2}$AF,
∴MN=PQ;
(2)解:当BD=$\frac{1}{3}$BC时,点M、点N、点P、点Q围成的四边形是矩形.
如图2,连结BE、MN、PQ,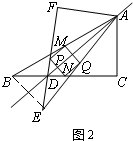 ,
,
∵点M、点Q是AB、AE的中点.
∴MQ∥BE且MQ=$\frac{1}{2}$BE,
∵点N是BC中点,
∴BN=$\frac{1}{2}$BC,
又∵BD=$\frac{1}{3}$BC,
∴DN=BN-BD=$\frac{1}{2}$BC-$\frac{1}{3}$BC=$\frac{1}{6}$BC,
∴$\frac{DN}{BD}$=$\frac{1}{2}$,
∵点B与点E关于直线AD对称,
∴BE⊥AD,
同理PN⊥AD,
∴BE∥PN,
∴△PDN∽△EDB,
∴$\frac{PN}{BE}$=$\frac{DN}{BD}$=$\frac{1}{2}$,
∴MQ∥PN且MQ=PN,
∴四边形MQNP是平行四边形,
∵MN=PQ,
∴四边形MQNP是矩形.
(3)由图形和(2)的结论可知,
当BD=0时,点M、点N、点P、点Q围成等腰三角形;
当0<BD<2时,点M、点N、点P、点Q围成等腰梯形;
当BD=2时,点M、点N、点P、点Q围成矩形;
当2<BD<3时,点M、点N、点P、点Q围成等腰梯形;
当BD=3时,点M、点N、点P、点Q围成等腰三角形;
当3<BD<6时,点M、点N、点P、点Q围成等腰梯形;
当BD=6时,点M、点N、点P、点Q围成矩形.
点评 本题考查的是相似三角形的判定和性质、矩形的判定和三角形中位线定理的应用,正确作出辅助线、灵活运用相关的定理是解题的关键.

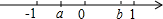 表示实数a,b的点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|.
表示实数a,b的点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|.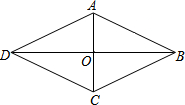 如图,在菱形ABCD中,AC,BD相交于O,若OA=$\frac{1}{2}$AD,则菱形的四个内角分别为多少度?
如图,在菱形ABCD中,AC,BD相交于O,若OA=$\frac{1}{2}$AD,则菱形的四个内角分别为多少度?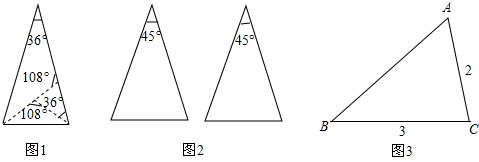
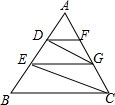 如图,DF∥EG,DG∥EC,DF∥BC,求证:AD:AE=AE:AB.
如图,DF∥EG,DG∥EC,DF∥BC,求证:AD:AE=AE:AB.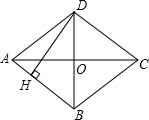 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH=$\frac{24}{5}$.
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH=$\frac{24}{5}$.