题目内容
9.已知a2-4a+9b2+6b+5=0,求a+b的值.分析 将原等式变形为两个平方式相加的形式,由偶次方的非负性可得出a、b的值,再将a、b的值代入到a+b中即可得出结论.
解答 解:∵a2-4a+9b2+6b+5=(a2-4a+4)+(9b2+6b+1)=(a-2)2+(3b+1)2=0,
∴有$\left\{\begin{array}{l}{a-2=0}\\{3b+1=0}\end{array}\right.$,即$\left\{\begin{array}{l}{a=2}\\{b=-\frac{1}{3}}\end{array}\right.$.
∴a+b=2+(-$\frac{1}{3}$)=$\frac{5}{3}$.
点评 本题考查了配方法的应用以及偶次方的非负性,解题的关键是将原式变形成两个平方式相加的形式.本题属于基础题,难度不大,解决该题型题目时,由偶次方的非负性求出各未知数的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
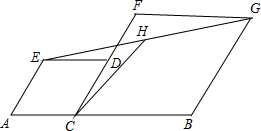 如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.
如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.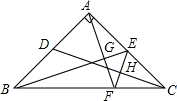 如图,在等腰三角形ABC中,∠BAC=90°,AB=AC,点D,E分别是AB,AC边上的中点,AF⊥BE交BC于点F,连接EF,交CD于点H,则下列结论:①∠FAE+∠EBF=45°;②$\frac{AG}{GE}$=$\frac{BG}{AG}$;③EF⊥CD;④CE=CF.其中结论正确的个数是( )
如图,在等腰三角形ABC中,∠BAC=90°,AB=AC,点D,E分别是AB,AC边上的中点,AF⊥BE交BC于点F,连接EF,交CD于点H,则下列结论:①∠FAE+∠EBF=45°;②$\frac{AG}{GE}$=$\frac{BG}{AG}$;③EF⊥CD;④CE=CF.其中结论正确的个数是( )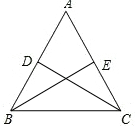 如图,D、E分别是AB、AC的中点,CD⊥AB,垂足为D,BE⊥AC,垂足为E,求证:AC=AB.
如图,D、E分别是AB、AC的中点,CD⊥AB,垂足为D,BE⊥AC,垂足为E,求证:AC=AB.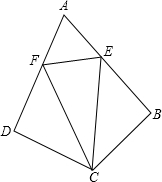 如图,在四边形ABCD中,∠ADC=∠ABC=90°,CB=CD,点E、F分别在AB、AD上,AE=AF,联结CE,CF.
如图,在四边形ABCD中,∠ADC=∠ABC=90°,CB=CD,点E、F分别在AB、AD上,AE=AF,联结CE,CF. 已知:如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=8cm.求:
已知:如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=8cm.求: