题目内容
1.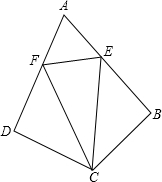 如图,在四边形ABCD中,∠ADC=∠ABC=90°,CB=CD,点E、F分别在AB、AD上,AE=AF,联结CE,CF.
如图,在四边形ABCD中,∠ADC=∠ABC=90°,CB=CD,点E、F分别在AB、AD上,AE=AF,联结CE,CF.(1)求证:CE=CF;
(2)如果∠BAD=60°,AF=2,CD=2$\sqrt{3}$,求△CEF的CE边长的高.
分析 (1)先证明△ACD≌△ACB,再证明△CAF≌△CAE即可.
(2)先求出CE的长,再求出△CEF的面积即可.
解答 (1)证明:连接AC,
∵∠ADC=∠ABC=90°,
在RT△ACD和RT△ACB中,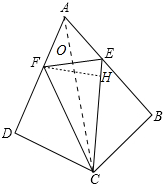
$\left\{\begin{array}{l}{AC=AC}\\{CD=CB}\end{array}\right.$,
∴△ACD≌△ACB,
∴∠CAF=∠CAE,
在△CAF和△CAE中,
$\left\{\begin{array}{l}{AF=AE}\\{∠CAF=∠CAE}\\{CA=CA}\end{array}\right.$,
∴△CAF≌△CAE,
∴CE=CF.
(2)设AC与EF交于点O,作FH⊥EC于H,
∵△ACD≌△ACB,∠DAB=60°,
∴AD=AB,∠CAD=∠CAB=30°,
在RT△ACD中,∵∠D=90°,CD=2$\sqrt{3}$,
∴AC=2CD=4$\sqrt{3}$,AD=$\sqrt{3}$CD=6
∵AF=AE,∠FAE=60°,
∴△AEF是等边三角形,
∴AF=AE=EF=2,DF=4,FC=EC=$\sqrt{D{F}^{2}+C{D}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{3})^{2}}$=2$\sqrt{7}$,
∴AO=$\sqrt{3}$,
∴CO=3$\sqrt{3}$,
∵S△EFC=$\frac{1}{2}$•EF•C0=$\frac{1}{2}$×2×3$\sqrt{3}$=3$\sqrt{3}$,
∵S△EFC=$\frac{1}{2}$•EC•FH,
∴3$\sqrt{3}$=$\frac{1}{2}$×$2\sqrt{7}$×FH,
∴FH=$\frac{3\sqrt{21}}{7}$.
点评 本题考查全等三角形的判定和性质、三角形的面积、勾股定理等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会转化的思想,求高想到求面积,属于中考常考题型.

 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数$y=\frac{k+1}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为3.
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数$y=\frac{k+1}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为3.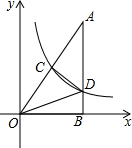 如图,在平面直角坐标系中,Rt△ABC的直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,交另一直角边于点D,连接CD,OCD的面积是3.
如图,在平面直角坐标系中,Rt△ABC的直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,交另一直角边于点D,连接CD,OCD的面积是3.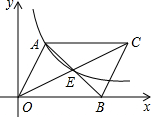 如图,?AOBC中,对角线交于点E,双曲线经过A、E两点,若?AOBC的面积为12,则k=4.
如图,?AOBC中,对角线交于点E,双曲线经过A、E两点,若?AOBC的面积为12,则k=4.