题目内容
19. 已知:如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=8cm.求:
已知:如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=8cm.求:(1)∠ABC的度数;
(2)对角线AC的长;
(3)菱形ABCD的面积.
分析 (1)根据菱形的性质得出AB=AD=BC=8cm,求出AD=2AE,即可得出∠ADE=30°,求出∠DAB=60°即可;
(2)过C作CM⊥AB,交AB延长线于M,根据勾股定理求出CM,求出AM,再根据勾股定理求出即可;
(3)根据菱形面积公式求出即可.
解答 解:(1)∵四边形ABCD是菱形,
∴AB=AD=BC=8cm,
∵DE⊥AB,E是AB的中点,
∴∠DEA=90°,AE=4cm,
∴AD=2AE,
∴∠ADE=30°,
∴∠DAB=60°,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠ABC+∠DAB=180°,
∴∠ABC=120°;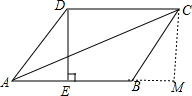 (2)过C作CM⊥AB,交AB延长线于M,
(2)过C作CM⊥AB,交AB延长线于M,
则∠M=90°,
∵BC=8cm,∠ABC=120°,
∴∠CBM=60°,
∴∠BCM=30°,
∴BM=$\frac{1}{2}$BC=4cm,
∴AM=8cm+4cm=12cm,
由勾股定理得:CM=$\sqrt{B{C}^{2}-B{M}^{2}}$=4$\sqrt{3}$cm,
AC=$\sqrt{C{M}^{2}+A{M}^{2}}$=$\sqrt{1{2}^{2}+(4\sqrt{3})^{2}}$=8$\sqrt{3}$(cm);
(3)菱形ABCD的面积为AB×CM=8cm×4$\sqrt{3}$cm=32$\sqrt{3}$cm2.
点评 本题考查了菱形的性质,勾股定理,三角形的面积的应用,能熟记菱形的性质是解此题的关键.

练习册系列答案
相关题目
4.在实数1,-2,0,-0.5中,最小的实数是( )
| A. | 1 | B. | -2 | C. | 0 | D. | -0.5 |
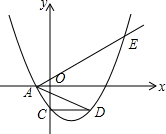 如图,抛物线y=$\frac{1}{{t}^{2}}$(x+t)(x-3t)交x轴负半轴于点A,交y轴于点C,点D,E均在抛物线上,且CD∥x轴,∠EAD=2∠ADC,求$\frac{AD}{AE}$的值.
如图,抛物线y=$\frac{1}{{t}^{2}}$(x+t)(x-3t)交x轴负半轴于点A,交y轴于点C,点D,E均在抛物线上,且CD∥x轴,∠EAD=2∠ADC,求$\frac{AD}{AE}$的值.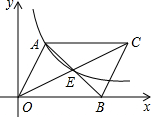 如图,?AOBC中,对角线交于点E,双曲线经过A、E两点,若?AOBC的面积为12,则k=4.
如图,?AOBC中,对角线交于点E,双曲线经过A、E两点,若?AOBC的面积为12,则k=4.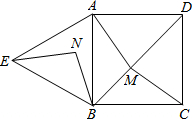 如图,△ABE是等边三角形,M是正方形ABCD对角线BD(不含B点)上任意一点,BM=BN,∠ABN=15°(点N在AB的左侧),当AM+BM+CM的最小值为$\sqrt{3}$+1时,正方形的边长为$\sqrt{2}$.
如图,△ABE是等边三角形,M是正方形ABCD对角线BD(不含B点)上任意一点,BM=BN,∠ABN=15°(点N在AB的左侧),当AM+BM+CM的最小值为$\sqrt{3}$+1时,正方形的边长为$\sqrt{2}$.