题目内容
已知抛物线y=x2+(2k+1)x-k2+k
(1)求证:此抛物线与x轴有两个不同的交点.
(2)当k=-1时,求此抛物线与x轴的交点坐标.
(1)求证:此抛物线与x轴有两个不同的交点.
(2)当k=-1时,求此抛物线与x轴的交点坐标.
考点:抛物线与x轴的交点
专题:
分析:(1)只需证明△=(2k+1)2-4(-k2+k)>0即可;
(2)将k=-1代入,令y=0求出抛物线与x轴的交点坐标.
(2)将k=-1代入,令y=0求出抛物线与x轴的交点坐标.
解答:解:(1)∵△=(2k+1)2-4(-k2+k)=4k+1-4k=1>0,
∴抛物线与x轴有两个不同的交点;
(2)当k=-1时,y=x2-x-2,
当y=0时,x2-x-2=0,
解得:x1=2,x2=-1,
即抛物线与x轴的交点坐标为(2,0),(-1,0).
∴抛物线与x轴有两个不同的交点;
(2)当k=-1时,y=x2-x-2,
当y=0时,x2-x-2=0,
解得:x1=2,x2=-1,
即抛物线与x轴的交点坐标为(2,0),(-1,0).
点评:本题考查了抛物线与x轴的交点,解答本题的关键是根据根的判别式△恒大于0证明抛物线与x轴有两个不同的交点.

练习册系列答案
相关题目
 如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.
如图,点O是四边形AEBC外接圆的圆心,点O在AB上,点P在BA的延长线上,且∠PEA=∠ADE,CD⊥AB于点H,交⊙O于点D.
 如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0
如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0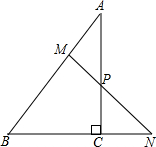 如图,在Rt△ABC中,∠ACB=90°,点P在AC边上,过P点作直线MN交BC延长线于N,交AB于M,且∠APM=∠A.
如图,在Rt△ABC中,∠ACB=90°,点P在AC边上,过P点作直线MN交BC延长线于N,交AB于M,且∠APM=∠A. 如图,△ABC中,∠C=90°,sinA=
如图,△ABC中,∠C=90°,sinA= 如图所示,二次函数y=x2-(a-2)x+a-5的图象交x轴于A和B,交y轴于C,当线段AB最短时,线段OC的长是
如图所示,二次函数y=x2-(a-2)x+a-5的图象交x轴于A和B,交y轴于C,当线段AB最短时,线段OC的长是 如图,在矩形ABCD中,AB=4,AD=10,直角尺的直角顶点P在AD上滑动时,(点P与A,D不重合),一直角边经过点C,另一直角边AB交于点E,是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
如图,在矩形ABCD中,AB=4,AD=10,直角尺的直角顶点P在AD上滑动时,(点P与A,D不重合),一直角边经过点C,另一直角边AB交于点E,是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由. 如图,△ABC中,∠BAC的平分线与边BC的垂直平分线交于点D,DE⊥AB于E,DF⊥AC于F,试猜想线段AB,AE,CF之间的数量关系,并证明.
如图,△ABC中,∠BAC的平分线与边BC的垂直平分线交于点D,DE⊥AB于E,DF⊥AC于F,试猜想线段AB,AE,CF之间的数量关系,并证明.