题目内容
 如图,在矩形ABCD中,AB=4,AD=10,直角尺的直角顶点P在AD上滑动时,(点P与A,D不重合),一直角边经过点C,另一直角边AB交于点E,是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
如图,在矩形ABCD中,AB=4,AD=10,直角尺的直角顶点P在AD上滑动时,(点P与A,D不重合),一直角边经过点C,另一直角边AB交于点E,是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.考点:相似三角形的判定与性质
专题:
分析:由于Rt△AEP∽Rt△DPC,当△DPC的周长等于△AEP周长的2倍时,两个三角形的相似比为1:2,可求出PD的长
解答:解:假设存在这样的点P,
∵Rt△AEP∽Rt△DPC,
∴
=
=
=2.
∵CD=AB=4,
∴AP=2,PD=8,
∴存在这样的P点,且DP长为8.
∵Rt△AEP∽Rt△DPC,
∴
| CD |
| AP |
| PD |
| AE |
| PC |
| PE |
∵CD=AB=4,
∴AP=2,PD=8,
∴存在这样的P点,且DP长为8.
点评:本题考查的是相似三角形和直角三角形的性质,属中学阶段的常规题.

练习册系列答案
相关题目
 新学期,两摞规格相同的数学课本整齐的叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:
新学期,两摞规格相同的数学课本整齐的叠放在讲台上,请根据图中所给出的数据信息,解答下列问题: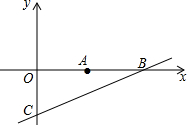 在平面直角坐标系xOy中,点A,点B,点C的坐标分别为(5,0),(10,0),(0,-5).
在平面直角坐标系xOy中,点A,点B,点C的坐标分别为(5,0),(10,0),(0,-5). 如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,求弦FC的长.
如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,求弦FC的长.