如图所示.二次函数y=x2-(a-2)x+a-5的图象交x轴于A和B.交y轴于C.当线段AB最短时.线段OC的长是．题目和参考答案——青夏教育精英家教网—

题目内容

如图所示，二次函数y=x²-（a-2）x+a-5的图象交x轴于A和B，交y轴于C，当线段AB最短时，线段OC的长是

．

考点：抛物线与x轴的交点

专题：

分析：令二次函数为0，根据根与系数的关系表示出AB的长度，求出当线段AB最短时a的值，最后代入a的值求出OC的长度．

解答：解：设点A坐标为（x₁，0），点B的坐标为（x₂，0），
令y=x²-（a-2）x+a-5=0，
则有x₁+x₂=a-2，x₁•x₂=a-5，
则AB=x₂-x₁=

(a-2)2-4(a-5)

(a-4)2+8

，
当a=4时，AB有最小值2

，
则OC=|a-5|=1．
故答案为：1．

点评：本题考查了抛物线与x轴的交点问题，解答本题的关键是根据根与系数的关系求出两根之和和两个之积．

练习册系列答案

相关题目

若a、b互为相反数，b、c互为倒数，并且m的立方等于它本身．
（1）试求

2a+2b

m+2

+ac值；
（2）若a＞1，b＜-1，且m＜0，S=|2a一3b|-2|b-m|-|b+

|，试求4（2a一S）+2（2a-S）-（2a-S）的值；
（3）若m≠0，当 x为有理数时，|x+m|-|x-m|存在最大值，请求出这个最大值（直接写出答案）．

已知抛物线y=x²+（2k+1）x-k²+k
（1）求证：此抛物线与x轴有两个不同的交点．
（2）当k=-1时，求此抛物线与x轴的交点坐标．

阅读下面材料：
定义：与圆的所有切线和割线都有公共点的几何图形叫做这个圆的关联图形．
问题：⊙O的半径为1，画一个⊙O的关联图形．
在解决这个问题时，小明以O为原点建立平面直角坐标系xOy进行探究，他发现能画出很多⊙O的关联图形，例如：⊙O本身和图1中的△ABC（它们都是封闭的图形），以及图2中以O为圆心的

DmE

（它是非封闭的形），它们都是⊙O的关联图形．而图2中以P，Q为端点的一条曲线就不是⊙O的关联图形．

参考小明的发现，解决问题：
（1）在下列几何图形中，⊙O的关联图形是

（填序号）；
①⊙O的外切正多边形；
②⊙O的内接正多边形；
③⊙O的一个半径大于1的同心圆．
（2）若图形G是⊙O的关联图形，并且它是封闭的，则图形G的周长的最小值是

；
（3）在图2中，当⊙O的关联图形

DmE

的弧长最小时，经过D，E两点的直线为y=

；
（4）请你在备用图中画出一个⊙O的关联图形，所画图形的长度l小于（2）中图形G的周长的最小值，并写出l的值（直接画出图形，不写作法）．

新学期，两摞规格相同的数学课本整齐的叠放在讲台上，请根据图中所给出的数据信息，解答下列问题：
（1）每本书的高度为

cm，课桌的高度为

cm；
（2）当课本数为x（本）时，请写出同样叠放在桌面上的一摞数学课本高出地面的距离（用含x的代数式表示）；
（3）桌面上有56本与题（1）中相同的数学课本，整齐叠放成一摞，若从中取走14本，求余下的数学课本高出地面的距离．

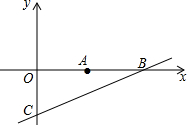在平面直角坐标系xOy中，点A，点B，点C的坐标分别为（5，0），（10，0），（0，-5）．
（1）求过点B，C两点的一次函数解析式；
（2）若直线BC上有一动点P（m，n），以点O，A，P为顶点的三角形面积相等，求P点坐标；
（3）若y轴上有一动点Q，使以点Q，A，C为顶点的三角形为等腰三角形，直接写出Q点坐标．

如图：⊙O的内接正方形ABCD，E为边CD上一点，且DE=CE，延长BE交⊙O于F，连结FC，若正方形边长为1，求弦FC的长．

如图所示，AB是⊙O的切线，切点为B，AO交⊙O于点C，过C点的切线交AB于点D．若AD=3BD，CD=2，求⊙O的半径．

试题分类