题目内容
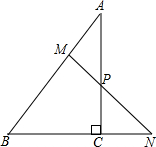 如图,在Rt△ABC中,∠ACB=90°,点P在AC边上,过P点作直线MN交BC延长线于N,交AB于M,且∠APM=∠A.
如图,在Rt△ABC中,∠ACB=90°,点P在AC边上,过P点作直线MN交BC延长线于N,交AB于M,且∠APM=∠A.求证:点M在BN的垂直平分线上.
考点:线段垂直平分线的性质
专题:证明题
分析:先根据两角互余的性质得出∠A+∠B=90°,∠N+∠CPN=90°,再由对顶角相等可得出∠CPN=∠APM,因为∠APM=∠A可知∠N+∠A=90°,故∠B=∠N,由此可得出结论.
解答:证明:∵∠ACB=90°,
∴∠A+∠B=90°,∠N+∠CPN=90°.
∵∠CPN与∠APM是对顶角,
∴∠CPN=∠APM.
∵∠APM=∠A,
∴∠N+∠A=90°,
∴∠B=∠N,即BM=MN,
∴点M在BN的垂直平分线上.
∴∠A+∠B=90°,∠N+∠CPN=90°.
∵∠CPN与∠APM是对顶角,
∴∠CPN=∠APM.
∵∠APM=∠A,
∴∠N+∠A=90°,
∴∠B=∠N,即BM=MN,
∴点M在BN的垂直平分线上.
点评:本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在同一平面内,两条直线的位置关系可能是( )
| A、相交或垂直 |
| B、垂直或平行 |
| C、平行或相交 |
| D、相交或垂直或平行 |

 在平面直角坐标系xOy中,点A,点B,点C的坐标分别为(5,0),(10,0),(0,-5).
在平面直角坐标系xOy中,点A,点B,点C的坐标分别为(5,0),(10,0),(0,-5).