题目内容
13.若abc>0.且a+b+c=0.则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$的值为-1.分析 根据题意确定出a,b,c中负数与正数个数,原式利用绝对值的代数意义化简即可得到结果.
解答 解:∵abc>0.且a+b+c=0,
∴a,b,c中有两个负数,
则原式=-1-1+1=-1,
故答案为:-1
点评 此题考查了有理数的除法,绝对值,以及有理数的乘法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
3. 如图,已知∠1=∠B,则下列结论不成立的是( )
如图,已知∠1=∠B,则下列结论不成立的是( )
 如图,已知∠1=∠B,则下列结论不成立的是( )
如图,已知∠1=∠B,则下列结论不成立的是( )| A. | AD∥BC | B. | ∠B=∠C | C. | ∠2+∠B=180° | D. | ∠1+∠2=180° |
18.3mn-2n2+1=2mn-______,横线上所填的式子是( )
| A. | 2m2-1 | B. | 2n2-mn+1 | C. | 2n2-mn-1 | D. | mn-2n2+1 |
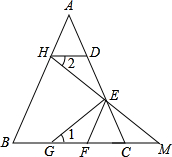 如图所示,在△ABC中,AB=AC,DE=EC,DH∥BA,EF∥AB,HE的延长线与BC的延长线相交于点M,点G在BC上,且∠1=∠2,证明:△EGM与△EFC是等腰三角形.
如图所示,在△ABC中,AB=AC,DE=EC,DH∥BA,EF∥AB,HE的延长线与BC的延长线相交于点M,点G在BC上,且∠1=∠2,证明:△EGM与△EFC是等腰三角形. 如图,数轴上点A表示$\sqrt{2}$,原点是线段AB的中点,设点B所表示的数为x,求x2+$\sqrt{2}x$的值.
如图,数轴上点A表示$\sqrt{2}$,原点是线段AB的中点,设点B所表示的数为x,求x2+$\sqrt{2}x$的值.