题目内容
1．将正方形ABCD的边BC延长线点E，使CE=AC，AE与DC相交于点F，则AE：AF=$\sqrt{2}$-1．分析 由四边形ABCD是正方形，得到AB=BC=AD，∠B=∠D=90°，根据等腰直角三角形的性质得到AC=$\sqrt{2}$BC，由已知条件得到BE=（1+$\sqrt{2}$）BC=（1+$\sqrt{2}$）AD，通过△ADF∽△EBA，得到比例式，即可得到结论．
解答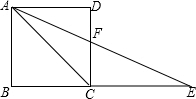 
解：∵四边形ABCD是正方形，
∴AB=BC=AD，∠B=∠D=90°，
∴AC=$\sqrt{2}$BC，
∵AC=CE，
∴BE=（1+$\sqrt{2}$）BC=（1+$\sqrt{2}$）AD，
∵AD∥BE，
∴∠DAF=∠E，
∴△ADF∽△EBA，
∴$\frac{AE}{AF}=\frac{AD}{BE}$=$\frac{1}{1+\sqrt{2}}$=$\sqrt{2}$-1．
故答案为：$\sqrt{2}$-1．
点评 本题考查了相似三角形的判定和性质，正方形的性质，等腰三角形的性质，熟记性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图：在△ABD中，已知AC⊥BD，AC=BC，CD=CE．求证：BF⊥AD．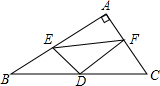
在Rt△ABC中，∠A=90°，点D为BC的中点，点E，F分别为AB，AC上的点，且ED⊥FD，以线段BE，EF，FC为边能否构成一个三角形？若能，请判断三角形的形状？
如图，在Rt△AOD中，∠AOD=90°，点 B，C在OD上，且OA=OB=BC=CD．求证：△ABC∽△DBA．