题目内容
19．先化简，后计算：3a+abc-$\frac{1}{3}{c^2}-3a+\frac{1}{3}{c^2}$，其中a=-2，b=$\frac{1}{2}$，c=-3．分析 首先对所求的式子合并同类项，然后代入数值计算即可．
解答 解：原式=abc，
则当a=-2，b=$\frac{1}{2}$，c=-3时，原式=-2×$\frac{1}{2}$×（-3）=3．
点评 本题考查了整式的化简求值，正确对整式进行合并同类项是关键．
练习册系列答案
相关题目
11．
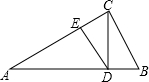如图，在Rt△ABC中，BC=a，AB=c，CD为斜边上的高，DE⊥AC．设△AED、△CDB、△ABC的周长分别为p1，p2，p，则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时，sinA=（ ）
如图，在Rt△ABC中，BC=a，AB=c，CD为斜边上的高，DE⊥AC．设△AED、△CDB、△ABC的周长分别为p1，p2，p，则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时，sinA=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{3}{4}$ |
9．
下列三角形中，一定和△ABC全等的是（ ）
下列三角形中，一定和△ABC全等的是（ ）| A． |  | B． |  | C． |  | D． |  |