题目内容
14.若两个实数的积是-1.则称这两个实数互为负倒数,如2与-$\frac{1}{2}$互为负倒数,(1)判断(4+$\sqrt{2}$)与(4-$\sqrt{2}$)是否互为负倒数,并说明理由;
(2)若实数($\sqrt{x}$+$\sqrt{y}$)是($\sqrt{x}$-$\sqrt{y}$)的负倒数,求点(x,y)中纵坐标随横坐标变化的函数解析式,并画出函数图象.
分析 (1)根据负倒数的定义判断即可;
(2)根据负倒数的定义列式计算求出x、y的关系,再根据一次函数的性质作出图象即可.
解答  解:(1)不互为负倒数,
解:(1)不互为负倒数,
理由如下:∵(4+$\sqrt{2}$)×(4-$\sqrt{2}$)=16-2=14≠-1,
∴(4+$\sqrt{2}$)与(4-$\sqrt{2}$)不互为负倒数;
(2)∵($\sqrt{x}$+$\sqrt{y}$)与($\sqrt{x}$-$\sqrt{y}$)互为负倒数,
∴($\sqrt{x}$+$\sqrt{y}$)×($\sqrt{x}$-$\sqrt{y}$)=-1,
∴x-y=-1,
y=x+1,
函数图象如图所示.
点评 本题考查了二次根式的应用,根据负倒数的定义以及一次函数的图象,读懂图目信息,理解并应用负倒数的定义进行计算是解题的关键.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
16. 如图,是二次函数 y=ax2+bx+c( a≠0 )的图象,则下列四个结论中正确的有几个?( )①abc>0; ②b2>4ac;③2c<3b;④4a+2b+c>0.
如图,是二次函数 y=ax2+bx+c( a≠0 )的图象,则下列四个结论中正确的有几个?( )①abc>0; ②b2>4ac;③2c<3b;④4a+2b+c>0.
 如图,是二次函数 y=ax2+bx+c( a≠0 )的图象,则下列四个结论中正确的有几个?( )①abc>0; ②b2>4ac;③2c<3b;④4a+2b+c>0.
如图,是二次函数 y=ax2+bx+c( a≠0 )的图象,则下列四个结论中正确的有几个?( )①abc>0; ②b2>4ac;③2c<3b;④4a+2b+c>0.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.下列因式分解正确的是( )
| A. | 4x2-4x+1=(1-2x)2 | B. | x2+2x-1=(x-1)2 | C. | -x2+(-2)2=(x-2)(x+2) | D. | x2-4x=2(x+2)(x-2) |
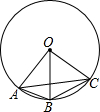 如图,点A、B、C均在⊙O上,且AB∥OC,若⊙O的半径为5,BC=6,则AC=8.
如图,点A、B、C均在⊙O上,且AB∥OC,若⊙O的半径为5,BC=6,则AC=8. 将如图所示的图形面积分成相等的两部分.
将如图所示的图形面积分成相等的两部分.