题目内容
9.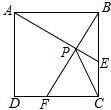 如图,在边长为$\sqrt{3}$的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
如图,在边长为$\sqrt{3}$的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
分析 首先判断出△ABE≌△BCF,即可判断出∠BAE=∠CBF,再根据∠BAE+∠BEA=90°,可得∠CBF+∠BEA=90°,所以∠APB=90°;然后根据点P在运动中保持∠APB=90°,可得点P的路径是一段以AB为直径的弧,设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,最后在Rt△BCG中,根据勾股定理,求出CG的长度,再求出PG的长度,即可求出线段CP的最小值为多少.
解答 解:如图,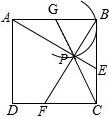 ,
,
∵动点F,E的速度相同,
∴DF=CE,
又∵CD=BC,
∴CF=BE,
在△ABE和△BCF中,
$\left\{\begin{array}{l}{AB=BC=\sqrt{3}}\\{∠ABE=BCF=90°}\\{BE=CF}\end{array}\right.$
∴△ABE≌△BCF,
∴∠BAE=∠CBF,
∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠APB=90°,
∵点P在运动中保持∠APB=90°,
∴点P的路径是一段以AB为直径的弧,
设AB的中点为G,连接CG交弧于点P,此时CP的长度最小,
在Rt△BCG中,CG=$\sqrt{{BC}^{2}{+BG}^{2}}=\sqrt{{(\sqrt{3})}^{2}{+(\frac{\sqrt{3}}{2})}^{2}}$=$\frac{\sqrt{15}}{2}$,
∵PG=$\frac{1}{2}AB=\frac{\sqrt{3}}{2}$
∴CP=CG-PG=$\frac{\sqrt{15}}{2}-\frac{\sqrt{3}}{2}$=$\frac{\sqrt{15}-\sqrt{3}}{2}$,
即线段CP的最小值为 $\frac{\sqrt{15}-\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{15}-\sqrt{3}}{2}$.
点评 (1)解答此题的关键是判断出什么情况下,CP的长度最小.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握,在判定三角形全等时,关键是选择恰当的判定条件.
(3)此题还考查了正方形的性质和应用,以及直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.

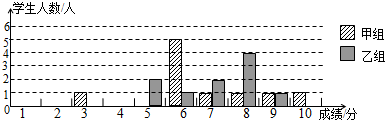
(1)补充完成下列的成绩统计分析表:
| 组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 甲 | 6.7 | 6 | 3.41 | 90% | 20% |
| 乙 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
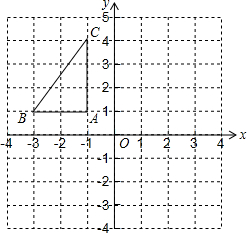 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为
 如图,已知∠A=∠F,∠C=∠D,那么BD∥CE吗?请说明理由.
如图,已知∠A=∠F,∠C=∠D,那么BD∥CE吗?请说明理由.