题目内容
14.在函数y=$\frac{1-x}{x-2}$中,自变量x的取值范围是x≠2.分析 求函数自变量的取值范围,就是求函数解析式有意义的条件,分式有意义的条件是:分母不为0.
解答 解:要使分式有意义,即:x-2≠0,
解得:x≠2.
故答案为:x≠2.
点评 本题主要考查函数自变量的取值范围,考查的知识点为:分式有意义,分母不为0.

练习册系列答案
相关题目
9.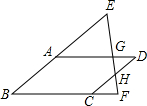 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )| A. | $\frac{EA}{BE}$=$\frac{EG}{EF}$ | B. | $\frac{EG}{GH}$=$\frac{AG}{GD}$ | C. | $\frac{AB}{AE}$=$\frac{BC}{CF}$ | D. | $\frac{FH}{EH}$=$\frac{CF}{AD}$ |
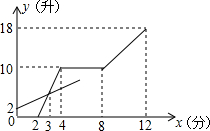 现有甲、乙两个容器,分别装有进水管和出水管,两容器的进出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.
现有甲、乙两个容器,分别装有进水管和出水管,两容器的进出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.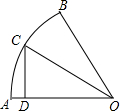 如图,在扇形OAB中,∠AOB=60°,扇形半径为r,点C在$\widehat{AB}$上,CD⊥OA,垂足为D,当△OCD的面积最大时,$\widehat{AC}$的长为$\frac{1}{4}πr$.
如图,在扇形OAB中,∠AOB=60°,扇形半径为r,点C在$\widehat{AB}$上,CD⊥OA,垂足为D,当△OCD的面积最大时,$\widehat{AC}$的长为$\frac{1}{4}πr$.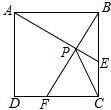 如图,在边长为$\sqrt{3}$的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
如图,在边长为$\sqrt{3}$的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为$\frac{\sqrt{15}-\sqrt{3}}{2}$.