题目内容
19.已知购买1个足球和1个篮球共需130元,购买2个足球和1个篮球共需180元.(1)求每个足球和每个篮球的进价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?
分析 (1)设每个篮球x元,每个足球y元,根据买1个篮球和2个足球共需180元,购买1个篮球和1个足球共需130元,列出方程组,求解即可;
(2)设买m个篮球,则购买(54-m)个足球,根据总价钱不超过4000元,列不等式求出x的最大整数解即可.
解答 解:(1)设每个篮球x元,每个足球y元,
由题意得,$\left\{\begin{array}{l}{x+y=130}\\{x+2y=180}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=80}\\{y=50}\end{array}\right.$,
答:每个篮球80元,每个足球50元;
(2)设买m个篮球,则购买(54-m)个足球,
由题意得,80m+50(54-m)≤4000,
解得:m≤$43\frac{1}{3}$,
∵m为整数,
∴m最大取43,
答:最多可以买43个篮球.
点评 本题考查了二元一次方程组的一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系,列方程求解.

练习册系列答案
相关题目
7.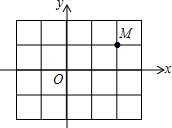 如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )
如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )
 如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )
如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )| A. | (2,-1) | B. | (2,3) | C. | (0,1) | D. | (4,1) |
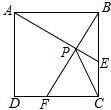 如图,在边长为$\sqrt{3}$的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
如图,在边长为$\sqrt{3}$的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
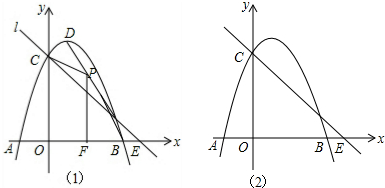
 如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点, 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=8cm,则⊙O的半径为4$\sqrt{2}$ cm.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=8cm,则⊙O的半径为4$\sqrt{2}$ cm.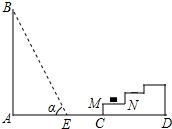 如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.($\sqrt{3}$取1.73)
如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.($\sqrt{3}$取1.73)