题目内容
14. 如图,在?ABCD中,点E在边AD上,AE:AD=2:3,BE与AC交于点F.若AC=15,则AF的长为6.
如图,在?ABCD中,点E在边AD上,AE:AD=2:3,BE与AC交于点F.若AC=15,则AF的长为6.
分析 根据四边形ABCD是平行四边形,证出△AEF∽△BCF,然后利用其对应边成比例即可求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴△AEF∽△BCF,
∴$\frac{AE}{BC}$=$\frac{AF}{CF}$,
∵?ABCD,
AD=BC,
∴$\frac{AE}{BC}=\frac{AE}{AD}=\frac{AF}{CF}=\frac{2}{3}$,
∵AC=15,即AF+CF=15,
∴AF=6,
故答案为:6.
点评 此题主要考查学生对相似三角形的判定与性质,平行四边形的性质等知识点,难度不大,属于基础题,能综合应用相似三角形的性质和平行四边形的性质是解题的关键.

练习册系列答案
相关题目
6.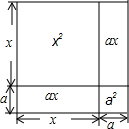 边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )
边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )
 边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )
边长为(x+a)的正方形如图所示,则这个正方形的面积不能表示为( )| A. | (x+a)(x+a) | B. | x2+a2+2ax | C. | 4(x+a) | D. | (x+a)a+(x+a)x |
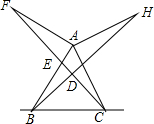 如图,已知AF=AB,AF⊥AB,AH=AC,AH⊥AC,连接CF,BH交于点D,求证:
如图,已知AF=AB,AF⊥AB,AH=AC,AH⊥AC,连接CF,BH交于点D,求证: 如图,在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,E为AB的中点,则∠ECD=30°.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,E为AB的中点,则∠ECD=30°.
 如图,在Rt△ABC中,∠C=90°,AC<BC.斜边AB的垂直平分线交边BC于点D.若BD=5,CD=3,则△ACD的周长是( )
如图,在Rt△ABC中,∠C=90°,AC<BC.斜边AB的垂直平分线交边BC于点D.若BD=5,CD=3,则△ACD的周长是( )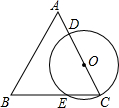 如图,△ABC是等边三角形,点O在边AC上(不与A,C重合),以点O为圆心,以OC为半径的圆分别与AC、BC相交于点D、E,若OC=1,则$\widehat{DE}$的长是$\frac{2π}{3}$(结果保留π).
如图,△ABC是等边三角形,点O在边AC上(不与A,C重合),以点O为圆心,以OC为半径的圆分别与AC、BC相交于点D、E,若OC=1,则$\widehat{DE}$的长是$\frac{2π}{3}$(结果保留π).