题目内容
5. 如图,在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,E为AB的中点,则∠ECD=30°.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°,E为AB的中点,则∠ECD=30°.
分析 根据直角三角形斜边上的中线求出CE=AE,求出∠ECA=∠A=30°,根据三角形内角和定理求出∠DCA,即可求出答案.
解答 解:∵在△ABC中,∠ACB=90°,E为AB的中点,
∴CE=AE=BE,
∴∠ECA=∠A,
∵∠A=30°,
∴∠ECA=30°,
∵CD⊥AB于D,
∴∠CDA=90°,
∵∠A=30°,
∴∠DCA=60°,
∴∠ECD=∠DCA-∠ECA=60°-30°=30°,
故答案为:30°.
点评 本题考查了直角三角形斜边上的中线,三角形内角和定理的应用,能求出AE=CE是解此题的关键,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
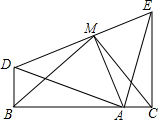 已知:如图,B、A、C三点共线,并且Rt△ABD≌Rt△ECA,M是DE的中点.
已知:如图,B、A、C三点共线,并且Rt△ABD≌Rt△ECA,M是DE的中点. 如图,已知l1∥l2∥l3,若AB:BC=3:5,DF=8,则DE=3.
如图,已知l1∥l2∥l3,若AB:BC=3:5,DF=8,则DE=3. 如图,在?ABCD中,点E在边AD上,AE:AD=2:3,BE与AC交于点F.若AC=15,则AF的长为6.
如图,在?ABCD中,点E在边AD上,AE:AD=2:3,BE与AC交于点F.若AC=15,则AF的长为6.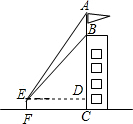 如图,为测量某建筑物BC上旗杆AB的高度,在离该建筑物底部12m的点F处,从E点观测旗杆的顶端A处和底端B处,视线与水平线夹角∠AED为52°,∠BED为45°,目高EF为1.6m.
如图,为测量某建筑物BC上旗杆AB的高度,在离该建筑物底部12m的点F处,从E点观测旗杆的顶端A处和底端B处,视线与水平线夹角∠AED为52°,∠BED为45°,目高EF为1.6m.