题目内容
某楼盘一楼是车库(暂不出售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为3000元/米2,从第八层起每上升一层,每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米.开发商为购买者制定了两种购房方案:
方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元)
(1)直接写出三楼售价为 元/米2,二十楼售价为 元/米2;
(2)请写出每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式.
(3)小张已筹到120000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
(4)有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元)
(1)直接写出三楼售价为
(2)请写出每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式.
(3)小张已筹到120000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
(4)有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
考点:一次函数的应用
专题:
分析:(1)根据楼层的价格变化,可得答案;
(2)分类讨论,2≤x≤8,8<x≤23,根据楼层的价格变化,可得函数解析式;
(3)分类讨论:2≤x≤8,8<x≤23,根据首付款与筹备款的不等式关系,可得答案;
(4)根据方案二的方法,可得房款的关系式,再根据不免物业费直接享受9%的优惠,可得函数关系式,再根据不等式的关系,可得答案.
(2)分类讨论,2≤x≤8,8<x≤23,根据楼层的价格变化,可得函数解析式;
(3)分类讨论:2≤x≤8,8<x≤23,根据首付款与筹备款的不等式关系,可得答案;
(4)根据方案二的方法,可得房款的关系式,再根据不免物业费直接享受9%的优惠,可得函数关系式,再根据不等式的关系,可得答案.
解答:解:(1)三楼售价为 2900 元/米2,二十楼售价为 3480 元/米2,
故答案为:2900,3480;
(2)每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式为
y=
;
(3)由(2)得当2≤x≤8时,(20x+2840)×120×30%=36(20x+2840)=36(20×8+2840)=108000<120000,
则2楼到8楼的楼层可任意选;
当8<x≤23时,(40x+2680)××30%=36(40x+2680)≤120000,
x<
,x是正整数,
8<x≤16,9层到6层任意楼层都可以购买,
综上所述,用方案一购房,他可以任意购买2层到16楼层的商品房;
(4)方案二y1=(40×16+2680)×120×(1-8%),
老王的想法y2=(40×16+2680)×120×(1-9%)+12×5a,
y1-y2=3984-60a
当y1>y2时,即y1-y2=3984-60a>0
0<a<60.4,想法正确,
当y1<y2时,y1-y2=3984-60a<0,
a>60.4,想法不正确,
因此,老王的说法不一定正确.
故答案为:2900,3480;
(2)每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式为
y=
|
(3)由(2)得当2≤x≤8时,(20x+2840)×120×30%=36(20x+2840)=36(20×8+2840)=108000<120000,
则2楼到8楼的楼层可任意选;
当8<x≤23时,(40x+2680)××30%=36(40x+2680)≤120000,
x<
| 49 |
| 3 |
8<x≤16,9层到6层任意楼层都可以购买,
综上所述,用方案一购房,他可以任意购买2层到16楼层的商品房;
(4)方案二y1=(40×16+2680)×120×(1-8%),
老王的想法y2=(40×16+2680)×120×(1-9%)+12×5a,
y1-y2=3984-60a
当y1>y2时,即y1-y2=3984-60a>0
0<a<60.4,想法正确,
当y1<y2时,y1-y2=3984-60a<0,
a>60.4,想法不正确,
因此,老王的说法不一定正确.
点评:本题考查了一次函数的应用,利用了分类讨论的思想,关键是求出函数的解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,AD⊥BC于D,AC=20,AB=15,AD=12.
如图,在△ABC中,AD⊥BC于D,AC=20,AB=15,AD=12. 某木工师傅制作如图的一个工件(阴影部分).
某木工师傅制作如图的一个工件(阴影部分). 如图,过点A画EF∥BC.
如图,过点A画EF∥BC.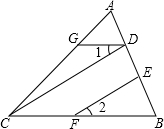 已知:如图,∠AGD=∠ACB,∠1=∠2,CD与EF平行吗?为什么?
已知:如图,∠AGD=∠ACB,∠1=∠2,CD与EF平行吗?为什么?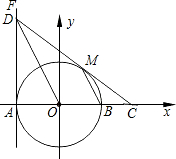 如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且点D的坐标为(-2,4),DO平行⊙O的弦MB,连DM并延长交x轴于点C.
如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且点D的坐标为(-2,4),DO平行⊙O的弦MB,连DM并延长交x轴于点C.