题目内容
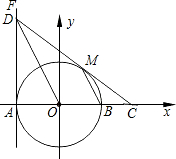 如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且点D的坐标为(-2,4),DO平行⊙O的弦MB,连DM并延长交x轴于点C.
如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且点D的坐标为(-2,4),DO平行⊙O的弦MB,连DM并延长交x轴于点C.(1)求点B的坐标;
(2)判断直线DC与⊙O的位置关系,并给出证明;
(3)若AC=2CM,求直线CD的解析式.
考点:圆的综合题
专题:
分析:(1)根据点D的坐标为(-2,4),求出OA的长,进而可得出B点坐标;
(2)通过证明三角形AOD和DOM全等来求解.已知的条件有OA=OM,一条公共边OD,只要证明出两组对应边的夹角相等即可,可通过OD∥MB,OM=OB来证得.
(3)先根据D点坐标求出AD的长,由切线的性质得出DM的长,在Rt△ADC中,AD的长已知,DC=DM+MC=DA+MC,那么可根据勾股定理和MC,AC的比例关系求出MC的长.也就求出了M的坐标.有了M和D的坐标可以用待定系数法求出DC所在直线的函数解析式.
(2)通过证明三角形AOD和DOM全等来求解.已知的条件有OA=OM,一条公共边OD,只要证明出两组对应边的夹角相等即可,可通过OD∥MB,OM=OB来证得.
(3)先根据D点坐标求出AD的长,由切线的性质得出DM的长,在Rt△ADC中,AD的长已知,DC=DM+MC=DA+MC,那么可根据勾股定理和MC,AC的比例关系求出MC的长.也就求出了M的坐标.有了M和D的坐标可以用待定系数法求出DC所在直线的函数解析式.
解答:(1)解:∵直线FA⊥x轴于点A,点D在FA上,且点D的坐标为(-2,4),
∴OA=2,
∴OB=OA=2,
∴B(2,0);
(2)答:直线DC与⊙O相切于点M.
证明如下:连OM,∵DO∥MB,
∴∠1=∠2,∠3=∠4.
∵OB=OM,
∴∠1=∠3.
∴∠2=∠4.
在△DAO与△DMO中,
,
∴△DAO≌△DMO(SAS).
∴∠OMD=∠OAD.
∵FA⊥x轴于点A,
∴∠OAD=90°.
∴∠OMD=90°.即OM⊥DC.
∴DC切⊙O于M.
(3)答:相切.
证明如下:∵D(-2,4),FA⊥x轴于点A,
∴AD=4,
∵DC切⊙O于M,
∴DM=AD=4,
在Rt△ACD中,
∵CD=MC+4,AC=2CM,
∴(2MC)2+42=(MC+4)2,解得MC=
或MC=0(不合题意,舍去).
∴MC的长为
.
∴点C(
,0).
设直线DC的解析式为y=kx+b.
则有
,
解得
.
∴直线DC的解析式为y=-
x+
.
∴OA=2,
∴OB=OA=2,
∴B(2,0);
(2)答:直线DC与⊙O相切于点M.
证明如下:连OM,∵DO∥MB,
∴∠1=∠2,∠3=∠4.
∵OB=OM,
∴∠1=∠3.
∴∠2=∠4.
在△DAO与△DMO中,
|
∴△DAO≌△DMO(SAS).
∴∠OMD=∠OAD.
∵FA⊥x轴于点A,
∴∠OAD=90°.
∴∠OMD=90°.即OM⊥DC.
∴DC切⊙O于M.
(3)答:相切.
证明如下:∵D(-2,4),FA⊥x轴于点A,
∴AD=4,
∵DC切⊙O于M,
∴DM=AD=4,
在Rt△ACD中,
∵CD=MC+4,AC=2CM,
∴(2MC)2+42=(MC+4)2,解得MC=
| 8 |
| 3 |
∴MC的长为
| 8 |
| 3 |
∴点C(
| 10 |
| 3 |
设直线DC的解析式为y=kx+b.
则有
|
解得
|
∴直线DC的解析式为y=-
| 3 |
| 4 |
| 5 |
| 2 |
点评:本题考查的是圆的综合题,涉及到切线的判定与性质、勾股定理及用待定系数法求一次函数的解析式等知识,难度适中.

练习册系列答案
相关题目
 如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
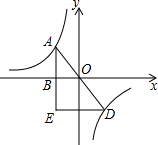 如图,反比例函数y1=
如图,反比例函数y1= 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=2,则DE的值为
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=2,则DE的值为