题目内容
11.已知a=$\sqrt{2}$+1,求代数式a2-2a+3的值.分析 将a的值代入原式=(a-1)2+2计算可得.
解答 解:当a=$\sqrt{2}$+1时,
原式=(a-1)2+2
=($\sqrt{2}$+1-1)2+2
=2+2
=4.
点评 本题主要考查二次根式的化简求值,根据代数式的特点将a的值代入变形后的式子是解题的关键.

练习册系列答案
相关题目
19.解方程:
(1)$\frac{1}{x+1}$+$\frac{2}{x-1}$=$\frac{4}{{{x^2}-1}}$
(2)$\frac{3}{x-2}$=$\frac{x}{2-x}$-2.
(1)$\frac{1}{x+1}$+$\frac{2}{x-1}$=$\frac{4}{{{x^2}-1}}$
(2)$\frac{3}{x-2}$=$\frac{x}{2-x}$-2.
16.二次函数 y=ax2+bx+c 的部分自变量和对应函数值如下:
当 x=3 时,y=-4.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -6.5 | -4 | -2.5 | -2 | -2.5 | … |
3. 如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )
如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )
 如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )
如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
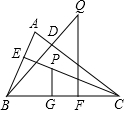 已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.
已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC. 如图,四边形ABCD∽四边形EFGH,连接对角线AC,EG.求证△ACD∽△EGH.
如图,四边形ABCD∽四边形EFGH,连接对角线AC,EG.求证△ACD∽△EGH.