题目内容
1.某商品现在的售价为每件60元,每月可卖出300件,经市场调查发现:每件商品涨价1元,每月少卖出10件,已知商品的进价为每件40元.(1)设每件这种商品涨价x元,商场销售这种商品每月盈利y元,求出y与x之间的函数关系式;
(2)这种商品每件涨多少元时才能使每月利润最大,最大利润为多少?
分析 (1)根据“总利润=单件利润×销售量”可列出函数解析式;
(2)由二次函数的顶点式可得其最值情况,即可解答.
解答 解:(1)根据题意可得:
y=(60-40+x)(300-10x)
=-10x2+100x+6000
=-10(x-5)2+6250;
∵300-10x≥0,
∴0≤x≤30;
(2)∵y=-10(x-5)2+6250,
∴当x=5时,y最大=6250,
答:这种商品每件涨5元时才能使每月利润最大,最大利润为6250元.
点评 本题主要考查二次函数的应用,熟练掌握销售问题中的相等关系:总利润=单件利润×销售量是列二次函数解析式解决问题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上). 如图已知直线CB∥OA,∠C=∠OAB=100°,点E、点F在线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.
如图已知直线CB∥OA,∠C=∠OAB=100°,点E、点F在线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.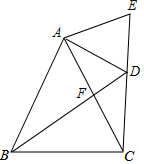 如图,△ABC中,AB=AC,点F为AC的中点,D为BF的延长线上一点,且∠BDC=∠BAC,E为CD的延长线上一点,且AD=AE,下列结论:①AD平分∠BDE;②CD=2DF;③BF=DF+DE;④S△ABC=2S四边形AEDF.其中结论正确的个数是( )
如图,△ABC中,AB=AC,点F为AC的中点,D为BF的延长线上一点,且∠BDC=∠BAC,E为CD的延长线上一点,且AD=AE,下列结论:①AD平分∠BDE;②CD=2DF;③BF=DF+DE;④S△ABC=2S四边形AEDF.其中结论正确的个数是( )