题目内容
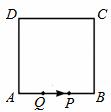
如图,在边长为4的正方形ABCD中,动点P,Q同时从A点出发,沿AB →BC→CD向D点运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,当P运动到D点时,P、Q
→BC→CD向D点运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,当P运动到D点时,P、Q 两点同时停止运动。设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系式是 。
两点同时停止运动。设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系式是 。
 。
。
【考点】动点问题的函数图象, 正方形的性质,分类和转换思想的应用。
正方形的性质,分类和转换思想的应用。
【分析】根据题意,动点P,Q运动的位置有三种形式:


点P,Q都在A B上,此时0≤t≤2,S=0
B上,此时0≤t≤2,S=0 。
。
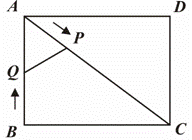
点P在BC上,点Q在AB上,如图1,此时2<t≤4,
由题意得, AQ=t,BP= ,
,
 。
。


∴
 。
。
综上所述,S与t的函数关系式是 。
。

练习册系列答案
相关题目
 OAC+S△OAB=
OAC+S△OAB=
 BC·r+
BC·r+

 别为AB=a,
别为AB=a, BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
BC=b,CD=c,AD=d,求四边形的内切圆半径r的值; 解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.
解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC分别相切于D、E和F,己知AD=3,BD=2,求r的值.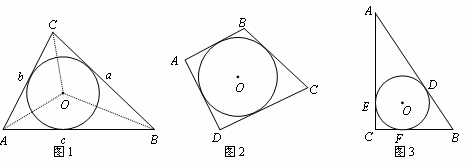

 过原点,与
过原点,与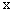 轴的另一个交点为B(4,0),A为抛物线C的顶点,直线OA的解析式为
轴的另一个交点为B(4,0),A为抛物线C的顶点,直线OA的解析式为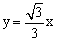 ,将抛物线C绕原点O旋转180°得到抛物线C1,求抛物线C、C1的解析式。
,将抛物线C绕原点O旋转180°得到抛物线C1,求抛物线C、C1的解析式。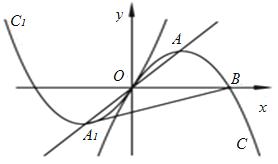
 该水平线自左向右匀速穿过矩形。设穿过的时间为t,矩形与三角形重合部分的面积为S,那么S关于t的函数大致图象应为 【 】
该水平线自左向右匀速穿过矩形。设穿过的时间为t,矩形与三角形重合部分的面积为S,那么S关于t的函数大致图象应为 【 】
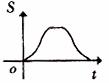 B.
B.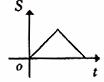 C.
C.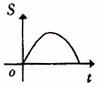 D.
D.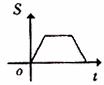


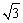 ),抛物线
),抛物线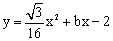 的图象过C点.
的图象过C点. :2的两部分?
:2的两部分?
 +1,AD=
+1,AD= 边形B′C′ED′,B′C′交AE于点F
边形B′C′ED′,B′C′交AE于点F ,则四边形B′FED′的面积为 ;
,则四边形B′FED′的面积为 ; ,将图
,将图 ②中的△AE
②中的△AE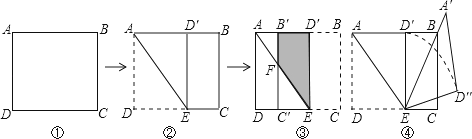



 P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究:
P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究: 是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由.