题目内容
如图，一根
木棒(AB)长为4，斜靠在与地面(OM)垂直的墙壁(ON)上，与地面的倾斜角(∠ABO)为60°，当木棒A端沿N0向下滑动到A′，B端沿直线OM向右滑动到B′，与地面的倾斜角(∠A′
B′O)为45°，则木棒中点从P随之运动到P′所经过的路径长为 。
。
【考点】直角三角形斜边上中线的性质，含30度角直角三角形的性质，等腰直角三角形的性质，弧长公式。
【分析】首先判断P运动到P′所经过的路径轨迹，由于P是木棒的中点，
根据直角三角形斜边上中线是斜边一半的性质，知轨迹是以OP=
AB为半径的圆弧，然后求出下滑形成的角度即可由弧长公式求得所求。
练习册系列答案
发散思维新课堂系列答案
相关题目
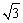），抛物线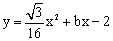
的图象过C点．
：2的两部分？
，且△ABC≌△DEF，将△DEF与△ABC重合在一起
，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点。探究：在△DEF运动过程中，重叠部分能否构成等
腰三角形？若
能，求出
△AEM的面积；若不能，请说明理由。
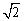AC。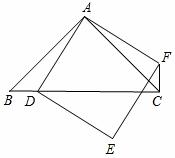
P（a，b）运动时，矩形PMON的面积为定值2．当点E，F都在线段AB上时，由三条线段AE，EF，BF组成一个三角形，记此三角形的外接圆面积为S1，△OEF的面积为S2．试探究：
是否存在最大值？若存在，请求出该最大值；若不存在，请说明理由．
）、B（0，3），点C是x轴上的一个动点，当
∠BCA=45°时，点C
的坐标为 
。
面积和为S1．
．
：
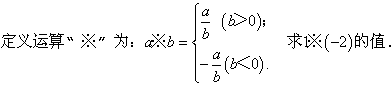
决问题的：由新定义可知a=1，b=-2，又b＜0，所以1※（-2）=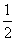
．
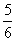
，则m= ．
函数y=2※x（x≠0）的图象大致是（
）
