题目内容
8.分解因式(1)25-4m2;
(2)x3-2x2+x;
(3)x2-4xy+4y2-4;
(4)x2(x-y)+(y-x).
分析 (1)直接利用平方差公式分解因式得出答案;
(2)首先提取公因式x,进而利用完全平方公式分解因式得出答案;
(3)首先将前三项分组进而利用完全平方公式分解因式,再利用平方差公式分解因式得出答案;
(4)首先提取公因式(x-y),进而利用平方差公式分解因式得出答案.
解答 解:(1)25-4m2=(5+2m)(5-2m);
(2)x3-2x2+x=x(x2-2x+1)
=x(x-1)2;
(3)x2-4xy+4y2-4
=(x-2y)2-4
=(x-2y+2)(x-2y-2);
(4)x2(x-y)+(y-x)
=(x-y)(x2-1)
=(x-y)(x+1)(x-1).
点评 此题主要考查了提取公因式法以及公式法分解因式,正确应用公式是解题关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
18. 如图,已知AF=2,点A,B分别是某函数图象与x轴,y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),当x=4时,P点的纵坐标为( )
如图,已知AF=2,点A,B分别是某函数图象与x轴,y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),当x=4时,P点的纵坐标为( )
 如图,已知AF=2,点A,B分别是某函数图象与x轴,y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),当x=4时,P点的纵坐标为( )
如图,已知AF=2,点A,B分别是某函数图象与x轴,y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),当x=4时,P点的纵坐标为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{69}}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{13}{5}$ |
19.已知四边形ABCD中,AB与CD不平行,AC与BD相交于点O,那么下列条件中能判定四边形ABCD是等腰梯形的是( )
| A. | AC=BD=BC | B. | AB=AD=CD | C. | OB=OC,AB=CD | D. | OB=OC,OA=OD |
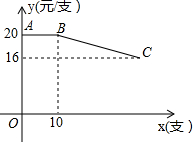 某文具专卖店专销某种品牌的钢笔,进价12元/支,售价20元/支,为了促销,专卖店决定:凡是一次性购买超过10支的,每超过一支,所购钢笔每支售价就降低0.20元,但是每支售价不能低于16元,如图线段AB和BC是购买钢笔的单价y(元/支)与购买数量x(支)的函数图象的一部分.
某文具专卖店专销某种品牌的钢笔,进价12元/支,售价20元/支,为了促销,专卖店决定:凡是一次性购买超过10支的,每超过一支,所购钢笔每支售价就降低0.20元,但是每支售价不能低于16元,如图线段AB和BC是购买钢笔的单价y(元/支)与购买数量x(支)的函数图象的一部分.