Question

16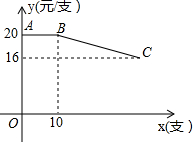．某文具专卖店专销某种品牌的钢笔，进价12元/支，售价20元/支，为了促销，专卖店决定：凡是一次性购买超过10支的，每超过一支，所购钢笔每支售价就降低0.20元，但是每支售价不能低于16元，如图线段AB和BC是购买钢笔的单价y（元/支）与购买数量x（支）的函数图象的一部分．
（1）顾客要想以最低价购买，需要一次至少购买30支（填最后结果）；
（2）当顾客一次购买x支时，求专卖店的利润w（元）与购买数量x（支）之间的函数关系式；
（3）求顾客一次购买多少支时，专卖店的利润是123.2元？

Answer 1

分析 （1）根据“凡是一次性购买超过10支的，每超过一支，所购钢笔每支售价就降低0.20元，但是每支售价不能低于16元”即可算出最少购买多少支时，价格为最低价；
（2）分0＜x≤10、10＜x≤30以及x＞30三种情况考虑，根据“利润=（售价-进价）×购买数量”即可得出w关于x的函数关系式；
（3）分别算出（2）中①的最大值以及③的最小值，即可得知专卖店的利润是123.2元时，只能是（2）中第②种情况，代入数据得出关于x的一元二次方程，解方程即可得出结论．

解答 解：（1）（20-16）÷0.2+10=30（支），
故答案为：30．
（2）购买数量x决定利润w（元）与购买数量x（支）的函数关系式，有3种情况：
①当0＜x≤10时，w=（20-12）x=8x；
②当10＜x≤30时，w=[20-0.2（x-10）-12]x=-0.2x²+10x；
③当x＞30时，w=（16-12）x=4x．
综上所述：w=$\left\{\begin{array}{l}{8x（0＜x≤10）}\\{-0.2{x}^{2}+10x（10＜x≤30）}\\{4x（x＞30）}\end{array}\right.$．
（3）∵当x=31时，w=124，124＞123.2；当x=10时，w=80，80＜123.2，
∴专卖店的利润是123.2元时，只能是（2）中第②种情况．
故-0.2x²+10x=123.2，即x²-50x+616=0，
解得：x₁=22，x₂=28．
答：顾客一次购买22支或28支时，专卖店的利润是123.2元．

点评 本题考查了二次函数的应用以及解一元二次方程，解题的关键是：（1）根据数量关系列式计算；（2）分0＜x≤10、10＜x≤30以及x＞30三种情况考虑，根据数量关系列出函数关系式；（3）代入数据得出关于x的一元二次方程．本题属于中档题，难度不大，解决该题型题目时，根据数量关系列出算式（函数关系式或方程）是关键．