题目内容
10.(1)两条直线相交于一点有2组不同的对顶角;(2)三条直线相交于一点有6组不同的对顶角;
(3)四条直线相交于一点有12组不同的对顶角;
(4)n条直线相交于同一点有n(n-1)组不同对顶角.(如图所示)
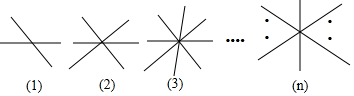
分析 根据(1)(2)(3)得出规律,可求n条直线相交于同一点有多少组不同对顶角.
解答 解:观察图形可知,n条直线相交于同一点有(1+2+…+n-1)×2=$\frac{n(n-1)}{2}$×2=n(n-1)组不同对顶角.
故答案为:n(n-1).
点评 考查了对顶角的定义,关键是熟悉对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.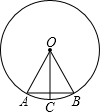 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论中,错误的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论中,错误的是( )
 如图,在⊙O中,OA=AB,OC⊥AB,则下列结论中,错误的是( )
如图,在⊙O中,OA=AB,OC⊥AB,则下列结论中,错误的是( )| A. | 弦AB的长等于圆内接正六边形的边长 | |
| B. | $\widehat{AC}$=$\widehat{BC}$ | |
| C. | 弦AC的长等于圆内接正十二边形的边长 | |
| D. | ∠BAC=30° |
3.已知甲数=2×2×3×5,乙数=2×3×3×5,那么甲数和乙数的最小公倍数是( )
| A. | 60 | B. | 90 | C. | 120 | D. | 180 |
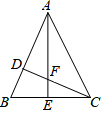 如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE.若S△ABC=12,△ADF的面积为S1,△CFE的面积为S2,则S1-S2=2.
如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE.若S△ABC=12,△ADF的面积为S1,△CFE的面积为S2,则S1-S2=2.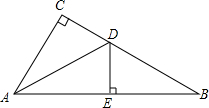 如图,在△ABC中,∠C=90°,∠B=30°,DE垂直平分AB,分别交BC,AB于点D,E,若AD=2,则BC=3.
如图,在△ABC中,∠C=90°,∠B=30°,DE垂直平分AB,分别交BC,AB于点D,E,若AD=2,则BC=3. 如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,求证:CA=CD.
如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,求证:CA=CD.