题目内容
18．
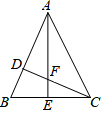如图，D、E分别是△ABC边AB、BC上的点，AD=2BD，BE=CE．若S△ABC=12，△ADF的面积为S1，△CFE的面积为S2，则S1-S2=2．
分析 S1-S2=S△ABE-S△BCD，所以求出△ABE的面积和△BCD的面积即可，因为AD=2BD，BE=CE，且S△ABC=12，就可以求出△ABE的面积和△BCD的面积．
解答 解：∵BE=CE，
∴BE=$\frac{1}{2}$BC，
∵S△ABC=12，
∴S△ABE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×12=6．
∵AD=2BD，S△ABC=12，
∴S△BCD=$\frac{1}{3}$S△ABC=4，
∵S△ABE-S△BCD=（S1+S四边形BEFD）-（S2+S四边形BEFD）=S1-S2，
即S1-S2=S△ABE-S△BCD=6-4=2．
故答案为2．
点评 本题考查三角形的面积，关键知道当高相等时，面积等于底边的比，根据此可求出三角形的面积，然后求出差．
练习册系列答案
相关题目
请认真观察图形，解答下列问题：
请你阅读小红同学的解题过程，并回答所提出的问题．
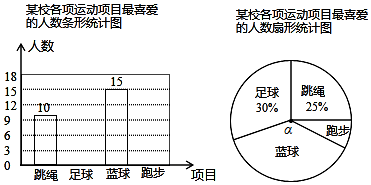
如图，在Rt△ABC中，∠ACB=90°，D、E、F分别是AB、BC、CA的中点，若CD=6cm，求EF的长．