题目内容
20.若a、b是等腰△ABC的两边,且a是不等式组$\left\{\begin{array}{l}{2(x-1)>3x-7}\\{\frac{1}{2}x-1>3-\frac{3}{2}x}\end{array}\right.$的最小整数解,b=46×0.256+(-$\frac{1}{2}$)-2-(3721-4568)0,求△ABC的周长.分析 解不等式组得到a=3,根据已知条件得到b=4,分类讨论即可得到结论.
解答 解:$\left\{\begin{array}{l}{2(x-1)>3x-7①}\\{\frac{1}{2}x-1>3-\frac{3}{2}x②}\end{array}\right.$
解不等式①,得x<5,
解不等式②,得x>2,
所以不等式组的解集是2<x<5,
因此,不等式组的最小整数解是3,即a=3,
∵b=46×0.256+(-$\frac{1}{2}$)-2-(3721-4568)0,
=(4×0.25)6+(-2)2-1=4,
当a=3为等腰三角形的底时,另外两腰都是b=4,
因为3+4=7,7大于4,能够成三角形
所以△ABC的周长是3+4+4=11,
当b=4为等腰三角形的底时,另外两腰都是a=3,
因为3+3=6,6大于4,能够成三角形
所以△ABC的周长是4+3+3=10,
所以△ABC的周长是10或11.
点评 此题主要考查了一元一次不等式组的应用和三角形三边关系等知识,利用已知得出分式中分子与分母的关系是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.已知x-y=-5,xy=3,则x2+y2=( )
| A. | -31 | B. | -25 | C. | 31 | D. | -19 |
15.某校在设立学生奖学金时规定:综合成绩最高分获得一等奖、综合成绩包括智育成绩、德育成绩、体育成绩三项,这三项成绩分别按60%、30%、10%的比例计入综合成绩.现有小天、小颖两位同学入选奖学金一等奖的评选,他们的智育成绩、德育成绩、体育成绩如表,请通过计算判断谁能拿到一等奖.
| 学生 | 体育成绩 | 德育成绩 | 学习成绩 |
| 小天 | 88分 | 84分 | 90分 |
| 小颖 | 90分 | 85分 | 88分 |
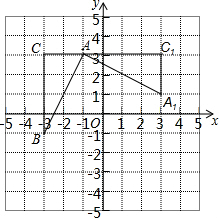 如图,在平面直角坐标系中,有一Rt△ABC,且点A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
如图,在平面直角坐标系中,有一Rt△ABC,且点A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的. 请认真观察图形,解答下列问题:
请认真观察图形,解答下列问题: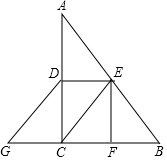 在△ABC中,∠ACB=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至点G,使CG=BF,连接CE,DE,DG.
在△ABC中,∠ACB=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至点G,使CG=BF,连接CE,DE,DG. 请你阅读小红同学的解题过程,并回答所提出的问题.
请你阅读小红同学的解题过程,并回答所提出的问题.