题目内容
15.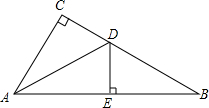 如图,在△ABC中,∠C=90°,∠B=30°,DE垂直平分AB,分别交BC,AB于点D,E,若AD=2,则BC=3.
如图,在△ABC中,∠C=90°,∠B=30°,DE垂直平分AB,分别交BC,AB于点D,E,若AD=2,则BC=3.
分析 根据三角形的内角和得到∠BAC=60°,根据角平分线的定义得到∠DAB=∠CAD=30°,得到AD=BD=2,CD=$\frac{1}{2}$AD=1,于是得到结论.
解答 解:∵∠C=90°,∠B=30°,
∴∠BAC=60°,
∵DE垂直平分AB,
∴∠DAB=∠CAD=30°,
∴∠DAB=∠B,
∴AD=BD=2,CD=$\frac{1}{2}$AD=1,
∴BC=CD+BD=3,
故答案为:3.
点评 本题考查了含30°角的直角三角形性质,等腰三角形的性质,熟练掌握直角三角形的性质是解题的关键.

练习册系列答案
相关题目
4. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )| A. | 两点之间,线段最短 | B. | 经过一点有无数条直线 | ||
| C. | 经过两点,有且只有一条直线 | D. | 部分小于总体 |
8.已知C是AB的中点,D是BC 的中点,下面等式不正确的是( )
| A. | CD=AC-DB | B. | CD=AD-BC | C. | CD=$\frac{1}{2}$AB-BD | D. | CD=$\frac{1}{3}$AB |
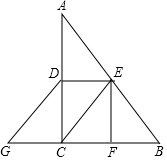 在△ABC中,∠ACB=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至点G,使CG=BF,连接CE,DE,DG.
在△ABC中,∠ACB=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至点G,使CG=BF,连接CE,DE,DG.
 如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=6cm,求EF的长.
如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=6cm,求EF的长.