题目内容
3. 如图,过圆O直径AB上的点C作AB的垂线交圆O于点D,再过D点作圆的切线l,然后过C点作l的垂线交l于点E,若AC=a,CB=b,那么CE长为( )
如图,过圆O直径AB上的点C作AB的垂线交圆O于点D,再过D点作圆的切线l,然后过C点作l的垂线交l于点E,若AC=a,CB=b,那么CE长为( )| A. | $\frac{2ab}{a+b}$ | B. | $\sqrt{ab}$ | C. | $\frac{a+b}{2}$ | D. | $\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$ |
分析 连接OD,如图,先表示出OD=$\frac{1}{2}$(a+b),OC=$\frac{1}{2}$(b-a),在利用勾股定理计算出CD=$\sqrt{ab}$,接着利用切线的性质得OD⊥l,则OD∥CE,所以∠ODC=∠ECD,然后证明Rt△ODC∽Rt△DCE,在利用相似比可计算出CE.
解答 解: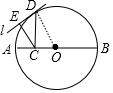 连接OD,如图,
连接OD,如图,
∵AB=AC+BC=a+b,
∴OD=$\frac{1}{2}$(a+b),
∴OC=$\frac{1}{2}$(a+b)-a=$\frac{1}{2}$(b-a)
∵CD⊥AB,
∴∠DCO=90°,
在Rt△DCO中,CD=$\sqrt{O{D}^{2}-O{C}^{2}}$=$\sqrt{ab}$,
∵l与⊙O相切于点D,
∴OD⊥l,
而CE⊥l,
∴OD∥CE,
∴∠ODC=∠ECD,
∴Rt△ODC∽Rt△DCE,
∴CD:CE=OD:CD,即$\sqrt{ab}$:CE=$\frac{1}{2}$(a+b):$\sqrt{ab}$,
∴CE=$\frac{2ab}{a+b}$.
故选A.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.由定理可知,若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.也考查了利用相似比计算线段的长.

练习册系列答案
相关题目
13.如表是一个三阶幻方,由9个数构成,且横行、竖行和对角线上的3个数的和都相等,试填出空格中的数.
| 3 | -7 | 7 |
| 5 | 1 | -3 |
| -5 | 9 | -1 |
14.下列命题中真命题是( )
| A. | 有理数都能表示成两个整数之比 | |
| B. | 各边相等的多边形是正多边形 | |
| C. | 等式两边同时乘以(或除以)同一个实数,所得结果仍是等式 | |
| D. | 相等的圆心角所对的弧相等,所对的弦相等 |
18.已知α为锐角,若tanα=$\frac{1}{2}$,则cosα等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
12.圆O1与圆O2半径分别为4和1,圆心距为2,作圆O2的切线,被圆O1所截得的最短弦长为( )
| A. | -1 | B. | 8 | C. | 2$\sqrt{7}$ | D. | 2$\sqrt{5}$ |
 已知如图所示,每个网格中的小正方形的边长都是1,图中的阴影部分是由三段以小正方形的顶点为圆心,半径分别是1和2的圆弧围成,则阴影部分的面积是$\frac{3π}{2}$-3.
已知如图所示,每个网格中的小正方形的边长都是1,图中的阴影部分是由三段以小正方形的顶点为圆心,半径分别是1和2的圆弧围成,则阴影部分的面积是$\frac{3π}{2}$-3.