题目内容
4.如图,四边形OABC为正方形,C的坐标为(0,4),点P为x轴正半轴上任意一点(与点O、A不重合),连接CP,CP的右侧作正方形CPGH,设OP=t(1)直接用含t的代数式表示点G的坐标为(t+4,t)
(2)过点G作GM∥x轴交射线OB于M,试判断线段GM的长度起否随t的变化而变化.若不变,求出其值;若变化,请说明理由;
(3)连接CG,交射线AB于E,求当t为何值时,E到B点的距离为1.
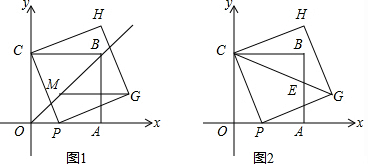
分析 (1)作GD⊥x轴于D,先根据正方形的性质,判定△GPD≌△PCO(AAS),得出GD=PO=t,DP=OC=4,进而得到OD=t+4,即点G的坐标为(t+4,t);
(2)连接AG,判定四边形ADGN是矩形,再判定四边形ADGN是正方形,得到∠GAD=45°=∠BOA,进而判定AG∥OM,再判定四边形OAGM是平行四边形,得出MG=OA=4,即线段MG的长度不发生改变;
(3)分两种情况讨论:①当E在线段AB上时,过点G作GD⊥x轴于D,作GF⊥AB于F;②当E在线段AB的延长线上时,过点G作GD⊥x轴于D,作GF⊥AB于F,分别判定四边形ADGF是正方形,得出GF=DG=AF=t,再根据CB∥GF,得出$\frac{EF}{EB}$=$\frac{FG}{BC}$,列出关于t的方程式,求得t的值即可.
解答  解:(1)如图1,作GD⊥x轴于D,
解:(1)如图1,作GD⊥x轴于D,
则∠GDP=90°,GD∥AB,
∴∠GPD+∠PGD=90°,
∵四边形PCHG是正方形,
∴∠CPG=90°,
∴∠GPD+∠CPO=90°,
∴∠PGD=∠CPO,
∵四边形AOCB是正方形,
∴∠POC=90°=∠GDP,OA=OC=AB=BC=4,∠BOA=45°,
在△GPD和△PCO中,
$\left\{\begin{array}{l}{∠POC=∠GDP}\\{∠CPO=∠PGD}\\{PC=GP}\end{array}\right.$,
∴△GPD≌△PCO(AAS),
∴GD=PO=t,DP=OC=4,
∴OD=t+4,
∴点G的坐标为:(t+4,t).
故答案为(t+4,t);
(2)线段MG的长度不发生改变.
理由:如图1,连接AG,
∵MG∥OA,GD∥AB,∠GDA=90°,
∴四边形ADGN是矩形,
又∵DP=OC=OA,
∴AD=PO=t=DG,
∴四边形ADGN是正方形,
∴∠GAD=45°=∠BOA,
∴AG∥OM,
∴四边形OAGM是平行四边形,
∴MG=OA=4,即线段MG的长度不发生改变;
(3)如图2,当E在线段AB上时,过点G作GD⊥x轴于D,作GF⊥AB于F,则四边形ADGF是矩形,
又∵DP=OC=OA=4,
∴AD=PO=t=DG,
∴四边形ADGF是正方形,
∴GF=DG=AF=t
又∵BE=1,
∴EF=4-1-t=3-t,
∵CB∥GF,
∴$\frac{EF}{EB}$=$\frac{FG}{BC}$,即$\frac{3-t}{1}=\frac{t}{4}$,
解得t=$\frac{12}{5}$;
如图3,当E在线段AB的延长线上时,过点G作GD⊥x轴于D,作GF⊥AB于F,则四边形ADGF是矩形,
又∵DP=OC=OA=4,
∴AD=PO=t=DG,
∴四边形ADGF是正方形,
∴GF=DG=AF=t
又∵BE=1,
∴EF=t-4-1=t-5,
∵CB∥GF,
∴$\frac{EF}{EB}$=$\frac{FG}{BC}$,即$\frac{t-5}{1}$=$\frac{t}{4}$,
解得t=$\frac{20}{3}$.
综上所述,当t为$\frac{12}{5}$或$\frac{20}{3}$时,E到B点的距离为1.
点评 本题主要考查了四边形的综合应用,解题时需要运用正方形的性质、平行四边形的判定与性质以及全等三角形的判定与性质,解决问题的关键是作辅助线构造平行线,利用平行线分线段成比例定理,列出方程式进行求解,解题时注意分类思想的运用.

| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
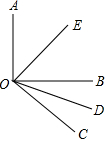 如图,OE是直角∠AOB的平分线,OD是∠BOC的平分线,若∠EOD=70°,求∠BOC的度数.
如图,OE是直角∠AOB的平分线,OD是∠BOC的平分线,若∠EOD=70°,求∠BOC的度数.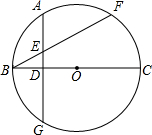 已知:如图,BC为⊙O的直径,BF为弦,A为$\widehat{BF}$的中点,AD⊥BC,垂足为D,AD和BF相交于点E,求证:AE=BE.
已知:如图,BC为⊙O的直径,BF为弦,A为$\widehat{BF}$的中点,AD⊥BC,垂足为D,AD和BF相交于点E,求证:AE=BE.