题目内容
10.已知一次函数y=kx+b(k≠0)经过点(0,3)和(-2,7),则y随x的增大而减小(填“增大”或“减小”).分析 直接把点(0,3)和(-2,7)代入一次函数y=kx+b(k≠0),求出k的值,进而可得出结论.
解答 解:∵一次函数y=kx+b(k≠0)经过点(0,3)和(-2,7),
∴$\left\{\begin{array}{l}{b=3}\\{-2k+b=7}\end{array}\right.$,解得k=-2<0,
∴y随x的增大而减小.
故答案为:减小.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 若|a|=-a,则a<0 | B. | 式子3xy2-4x3y+12是七次三项式 | ||
| C. | 若a<0,ab<0,则b>0 | D. | 若a=b,m是有理数,则$\frac{a}{m}$=$\frac{b}{m}$ |
15.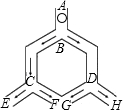 如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
 如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )
如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
19.若m,n为任意实数,则下列各式成立的是( )
| A. | $\sqrt{(m+n)^{2}}$=m+n | B. | $\sqrt{{m}^{2}}$+$\sqrt{{n}^{2}}$=m+n | C. | $\sqrt{mn}$=$\sqrt{m}+\sqrt{n}$ | D. | $\sqrt{(m+n)^{4}}=(m+n)^{2}$ |
20.某人去水果批发市场采购苹果,他看中了A、B两家苹果.这两家苹果品质都一样,零售价都为6元/千克,但批发价各不相同.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如表:
【表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500)】
根据上述信息,请解答下列问题:
(1)如果他批发1000千克苹果,则他在A 家批发需要5520元,在B家批发需要5400元;
(2)如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要5.4x元,在B家批发需要4.5x+1200元(用含x的代数式表示);
(3)现在他要批发不超过1000千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如表:
| 数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
| 价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
根据上述信息,请解答下列问题:
(1)如果他批发1000千克苹果,则他在A 家批发需要5520元,在B家批发需要5400元;
(2)如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要5.4x元,在B家批发需要4.5x+1200元(用含x的代数式表示);
(3)现在他要批发不超过1000千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
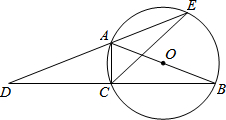 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.