题目内容
10.平面内n条直线,每两条直线都相交,最少有1个交点,最多有$\frac{n(n-1)}{2}$个交点.分析 分别求出2条、3条、4条、5条、6条直线相交时最多的交点个数,找出规律即可解答.
解答 解:2条直线相交最多有1个交点;
3条直线相交最多有1+2个交点;
4条直线相交最多有1+2+3个交点;
5条直线相交最多有1+2+3+4个交点;
6条直线相交最多有1+2+3+4+5个交点;
…
n条直线相交最多有1+2+3+4+5+…+(n-1)=$\frac{n(n-1)}{2}$个交点;
n条直线相交与一点,最少有1个交点,
故答案为:1,$\frac{n(n-1)}{2}$.
点评 本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n条直线相交最多有n(n-1)÷2个交点.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
20.若A、B、C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离( )
| A. | 等于4cm | B. | 大于4cm而小于5cm | ||
| C. | 不大于4cm | D. | 小于4cm |
5.下列说法正确的是( )
| A. | 有且只有一条直线垂直于已知直线 | |
| B. | 互相垂直的直线一定相交 | |
| C. | 从直线外一点到这条直线的垂线段叫做点到直线的距离 | |
| D. | 直线L外一点P与直线L上各点连接而成的线段中最短线段的长度是3cm,则点P到直线L的距离是3cm. |
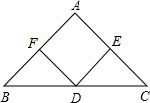 如图,在△ABC中,点D,E,F分别是边BC,CA,AB的中点,使四边形AFDE为菱形,应添加的条件是AF=AE(添加一个条件即可).
如图,在△ABC中,点D,E,F分别是边BC,CA,AB的中点,使四边形AFDE为菱形,应添加的条件是AF=AE(添加一个条件即可).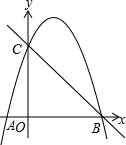 如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.
如图,抛物线y=ax2+3x+c经过A(-1,0),B(4,0)两点,与y轴交于点C.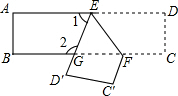 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在D′、C′的位置上.如图所示,若∠EFG=60°,求∠1与∠2的度数.
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在D′、C′的位置上.如图所示,若∠EFG=60°,求∠1与∠2的度数.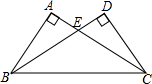 如图,∠BAC=90°,∠EDC=90°,∠DCE=30°,ED=2,AB=3,求S△CEB的值.
如图,∠BAC=90°,∠EDC=90°,∠DCE=30°,ED=2,AB=3,求S△CEB的值.