题目内容
8.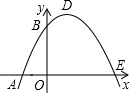 如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)
如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)当点D在第一象限的抛物线上运动时,(2)中四边形AEDB的面积是否最大?若是,请说明理由;若不是,请求出四边形AEDB面积的最大值.
分析 (1)由抛物线与x轴的两个交点可设抛物线的解析式为y=a(x+1)(x-3),将点B的坐标代入抛物线解析式中求出a值即可;
(2)连接OD,将抛物线解析式变形为顶点式即可得出点D的坐标,利用三角形的面积结合S四边形AEDB=S△AOB+S△OBO+S△OED即可得出结论;
(3)连接BE,过点D作DF⊥x轴交BE于点F,由点B、E的坐标利用待定系数法即可求出直线BE的解析式,设D的坐标为(a,-a2+2a+3)(0<a<3),则点F的坐标为(a,-a+3),从而找出DF的长度,再根据三角形的面积结合S四边形AEDB=S△BDE+S△AEB即可得出S四边形AEDB=-$\frac{3}{2}$$(a-\frac{3}{2})^{2}$+$\frac{75}{8}$,利用二次函数的性质即可解决最值问题.
解答 解:(1)设抛物线的解析式为y=a(x+1)(x-3),
将B(0,3)代入y=a(x+1)(x-3),
3=-3a,解得:a=-1,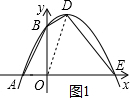
∴抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3.
(2)连接OD,如图1所示.
∵y=-x2+2x+3=-(x-1)2+4,
∴点D(1,4),
∴S四边形AEDB=S△AOB+S△OBO+S△OED=$\frac{1}{2}$×(1×3+3×1+3×4)=9.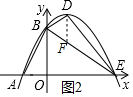
(3)连接BE,过点D作DF⊥x轴交BE于点F,如图2所示.
设直线BE的解析式为y=kx+b,
将B(0,3)、E(3,0)代入y=kx+b,
$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BE的解析式为y=-x+3.
设D的坐标为(a,-a2+2a+3)(0<a<3),则点F的坐标为(a,-a+3),
∴DF=-a2+2a+3-(-a+3)=-a2+3a=-$(a-\frac{3}{2})^{2}$+$\frac{9}{4}$,
∴S△BDE=$\frac{1}{2}$OE•DF=-$\frac{3}{2}$$(a-\frac{3}{2})^{2}$+$\frac{27}{8}$.
∴S四边形AEDB=S△BDE+S△AEB=-$\frac{3}{2}$$(a-\frac{3}{2})^{2}$+$\frac{27}{8}$+6=-$\frac{3}{2}$$(a-\frac{3}{2})^{2}$+$\frac{75}{8}$.
∴当a=$\frac{3}{2}$时,S四边形AEDB=取最大值,最大值为$\frac{75}{8}$.
故当点D在第一象限的抛物线上运动时,(2)中四边形AEDB的面积不是最大,四边形AEDB面积的最大值为$\frac{75}{8}$.
点评 本题考查了抛物线与x轴的交点、二次函数的最值、待定系数法求一次(二次)函数解析式以及三角形的面积,解题的关键是:(1)根据点的坐标利用待定系数法求出二次函数解析式;(2)利用三角形的面积结合S四边形AEDB=S△AOB+S△OBO+S△OED求出四边形AEDB的面积;(3)找出S四边形AEDB=-$\frac{3}{2}$$(a-\frac{3}{2})^{2}$+$\frac{75}{8}$,利用二次函数的性质解决最值问题.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
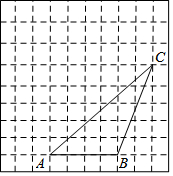 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度. 如图,AD是等边三角形BC边上的高,以AD为边作等边三角形△ADE,连结BE.
如图,AD是等边三角形BC边上的高,以AD为边作等边三角形△ADE,连结BE. 如图,点A2,A4,A6,…分别是射线OM上的点,点A1,A3,A5,…分别是y轴正半轴上的点,△OA1A2,△OA2A3,△OA3A4,…分别是以OA2,OA3,OA4…为底边的等腰三角形,若OM与x轴正半轴的夹角为60°,OA1=1,则可求得点A6的坐标为($\frac{9\sqrt{3}}{2}$,$\frac{27}{2}$),点A2n的坐标为($\frac{1}{2}$$(\sqrt{3})^{2n-1}$,$\frac{1}{2}$$(\sqrt{3})^{2n}$).
如图,点A2,A4,A6,…分别是射线OM上的点,点A1,A3,A5,…分别是y轴正半轴上的点,△OA1A2,△OA2A3,△OA3A4,…分别是以OA2,OA3,OA4…为底边的等腰三角形,若OM与x轴正半轴的夹角为60°,OA1=1,则可求得点A6的坐标为($\frac{9\sqrt{3}}{2}$,$\frac{27}{2}$),点A2n的坐标为($\frac{1}{2}$$(\sqrt{3})^{2n-1}$,$\frac{1}{2}$$(\sqrt{3})^{2n}$). 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2)
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2)