题目内容
12．已知a2-3a-3=0，求代数式$\frac{{a}^{3}}{{a}^{2}+2a+1}$÷（1-$\frac{1}{a+1}$）的值．分析 先把括号内通分和除法运算化为乘法运算，再把a2+2a+1分解因式，然后约分得到原式=$\frac{{a}^{2}}{a+1}$，再利用已知条件变形得到a2=3a+3，接着利用整体代入的方法计算．
解答 解：$\frac{{a}^{3}}{{a}^{2}+2a+1}$÷（1-$\frac{1}{a+1}$）
=$\frac{{a}^{3}}{（a+1）^{2}}$÷（$\frac{a+1-1}{a+1}$）
=$\frac{{a}^{3}}{（a+1）^{2}}$•$\frac{a+1}{a}$
=$\frac{{a}^{2}}{a+1}$，
∵a2-3a-3=0，
∴a2=3（a+1），
∴原式=$\frac{3（a+1）}{a+1}$=3．
点评 本题考查了分式的化简求值：先把分式的分子或分母因式分解，再进行通分或约分，得到最简分式或整式，然后把满足条件的字母的值代入计算得到对应的分式的值．
练习册系列答案
相关题目
如图，已知A（-3，n），B（2，-3）是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点．
如图，AD是等边三角形BC边上的高，以AD为边作等边三角形△ADE，连结BE．
如图，点A2，A4，A6，…分别是射线OM上的点，点A1，A3，A5，…分别是y轴正半轴上的点，△OA1A2，△OA2A3，△OA3A4，…分别是以OA2，OA3，OA4…为底边的等腰三角形，若OM与x轴正半轴的夹角为60°，OA1=1，则可求得点A6的坐标为（$\frac{9\sqrt{3}}{2}$，$\frac{27}{2}$），点A2n的坐标为（$\frac{1}{2}$$（\sqrt{3}）^{2n-1}$，$\frac{1}{2}$$（\sqrt{3}）^{2n}$）．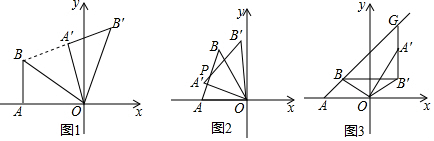
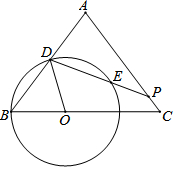如图，已知△ABC中，AB=AC=5，BC=6，点O是边BC上的动点，以点O为圆心，OB为半径作圆O，交AB边于点D，过点D作∠ODP=∠B，交边AC于点P，交圆O与点E．设OB=x．