题目内容
10.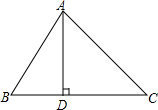 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.(1)求∠BAC的度数;
(2)若AB=4,求BC的长.
分析 (1)在Rt△ABD和Rt△ADC中,分别求出∠BAD,∠DAC即可解决问题;
(2)分别解直角三角形求出BD、AD、DC即可解决问题;
解答 解:(1)∵AD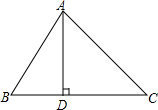 ⊥BC,
⊥BC,
∴∠ADB=∠ADC=90°,
∵∠B=60°,∠C=45°,
∴∠BAD=90°-60°=30°,∠DAC=90°-45°=45°,
∴∠BAC=∠BAD+∠DAC=75°.
(2)在Rt△ABD中,∵AB=4,∠BAD=30°,
∴BD=$\frac{1}{2}$AB=2,AD=$\sqrt{3}$BD=2$\sqrt{3}$,
∴DC=AD=2$\sqrt{3}$,
∴BC=BD+DC=2+2$\sqrt{3}$.
点评 本题考查直角三角形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.在?ABCD中,对角线AC、BD交于点O,添加下列的条件还不能使?ABCD是菱形的是( )
| A. | AB=BC | B. | AC⊥BD | C. | OA=OC | D. | AC平分∠BAD |
20.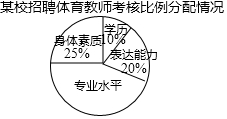 为贯彻国务院办公厅发布的《中国足球发展改革总体方案》精神,某校准备招聘一名足球专业的体育老师,该校对甲、乙、丙三名应聘者从学历、专业水平、身体素质、表达能力等四个方面考核打分,每一方面满分10分,得分情况如下表(单位:分),考核比例分配情况见扇形统计图.
为贯彻国务院办公厅发布的《中国足球发展改革总体方案》精神,某校准备招聘一名足球专业的体育老师,该校对甲、乙、丙三名应聘者从学历、专业水平、身体素质、表达能力等四个方面考核打分,每一方面满分10分,得分情况如下表(单位:分),考核比例分配情况见扇形统计图.
某校应聘体育教师考核得分情况
(1)在扇形统计图中,求“专业水平”所占圆心角度数;
(2)运用统计知识分析该校应该录取哪一位应聘者;
(3)请对落聘者提出合理化建议.
 为贯彻国务院办公厅发布的《中国足球发展改革总体方案》精神,某校准备招聘一名足球专业的体育老师,该校对甲、乙、丙三名应聘者从学历、专业水平、身体素质、表达能力等四个方面考核打分,每一方面满分10分,得分情况如下表(单位:分),考核比例分配情况见扇形统计图.
为贯彻国务院办公厅发布的《中国足球发展改革总体方案》精神,某校准备招聘一名足球专业的体育老师,该校对甲、乙、丙三名应聘者从学历、专业水平、身体素质、表达能力等四个方面考核打分,每一方面满分10分,得分情况如下表(单位:分),考核比例分配情况见扇形统计图.某校应聘体育教师考核得分情况
| 甲 | 乙 | 丙 | |
| 学历 | 8 | 9 | 8 |
| 专业水平 | 9 | 8 | 9 |
| 身体素质 | 8 | 7 | 6 |
| 表达能力 | 7 | 8 | 9 |
(2)运用统计知识分析该校应该录取哪一位应聘者;
(3)请对落聘者提出合理化建议.
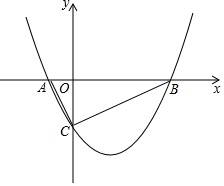 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴相交于点A、B,与y轴相交于点C,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴相交于点A、B,与y轴相交于点C,且A(-1,0). 如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.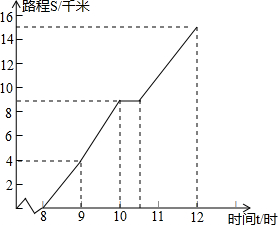 为一位旅行者在早晨8时从城市出发到郊外所走的路程s(km)与时间t(时)的变量关系的图象.根据图象回答问题:
为一位旅行者在早晨8时从城市出发到郊外所走的路程s(km)与时间t(时)的变量关系的图象.根据图象回答问题: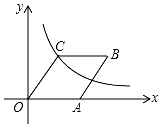 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).