题目内容
如图，已知?ABCD中，点E为BC延长线上的点，若S?ABCD=20cm2，S△CEF=9cm2，则S△ADF=考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：设CE：BC=CE：AD=x，根据相似三角形面积的比等于相似比的平方得到S△CEF：S△ABE=x2：（1+x）2，S△CEF：S△ADF=x2：1，根据S△ABE+S△ADF=SABCD+S△CEF列出（1+x）2：x2+1：x2=（20+9）：9后即可解得：x=
，从而求得S△ADF=S△CEF：x2=4cm2．
| 3 |
| 2 |
解答：解：设CE：BC=CE：AD=x
则有S△CEF：S△ABE=x2：（1+x）2，
S△CEF：S△ADF=x2：1
而S△ABE+S△ADF=SABCD+S△CEF
因此有（1+x）2：x2+1：x2=（20+9）：9
得到x=
，
从而S△ADF=S△CEF：x2=4cm2．
故答案为：4cm2．
则有S△CEF：S△ABE=x2：（1+x）2，
S△CEF：S△ADF=x2：1
而S△ABE+S△ADF=SABCD+S△CEF
因此有（1+x）2：x2+1：x2=（20+9）：9
得到x=
| 3 |
| 2 |
从而S△ADF=S△CEF：x2=4cm2．
故答案为：4cm2．
点评：本题考查了相似三角形的判定与性质及平行四边形的性质，解题的关键是正确的设出未知数并利用面积的比等于相似比的平方确定答案．
练习册系列答案
名校课堂系列答案
相关题目
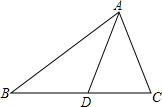如图，在△ABC中，D是BC上一点，证明：AB+BC+AC＞2CD．
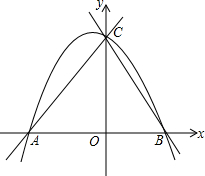如图，二次函数y=ax2+2ax+4的图象与x轴交于点A、B，与y轴交于点C，OC：OB=2：1，