题目内容
 阅读下列内容:
阅读下列内容:为了求tan15°的值,可构造如图所示的直角三角形:作Rt△ABC,使∠C=90°,∠ABC=30°,延长CB到点D,使BD=AB,得∠D=15°,设AC=k,则AB=BD=2k,BC=
| 3 |
| AC |
| CD |
| k | ||
(2+
|
| 1 | ||
2+
|
| 3 |
考点:解直角三角形
专题:阅读型
分析:同样按阅读内容作Rt△ABC,使∠C=90°,∠ABC=45°,延长CB到D,使BD=AB,连接AD,根据构造的直角三角形,设AC=k,再用k表示出CD,即可求出tan22.5°的值.
解答: 解:作Rt△ABC,使∠C=90°,∠ABC=45°,如图.
解:作Rt△ABC,使∠C=90°,∠ABC=45°,如图.
延长CB到D,使BD=AB,连接AD,则∠D=
∠ABC=22.5°.
设AC=k,则BC=k,AB=BD=
k.
又∵CD=BD+CB=(
+1)k,
∴tan22.5°=tan∠D=
=
=
-1.
 解:作Rt△ABC,使∠C=90°,∠ABC=45°,如图.
解:作Rt△ABC,使∠C=90°,∠ABC=45°,如图.延长CB到D,使BD=AB,连接AD,则∠D=
| 1 |
| 2 |
设AC=k,则BC=k,AB=BD=
| 2 |
又∵CD=BD+CB=(
| 2 |
∴tan22.5°=tan∠D=
| AC |
| CD |
| k | ||
(
|
| 2 |
点评:此题考查的是解直角三角形,关键是根据阅读构造含45°的直角三角形,再作辅助线得22.5°角的直角三角形,再设AC=k,用k表示出CD.

练习册系列答案
相关题目
 实数a在数轴上的位置如图所示,则
实数a在数轴上的位置如图所示,则| (a-3)2 |
| (a-9)2 |
| A、6 | B、-6 |
| C、2a-12 | D、无法确定 |
 (1)请将图中的角用不同方法表示出来,并填写下表:
(1)请将图中的角用不同方法表示出来,并填写下表: 如图,在Rt△ABC中,已知∠B=90°,∠C=30°,点D是BC的中点,求sin∠DAC.
如图,在Rt△ABC中,已知∠B=90°,∠C=30°,点D是BC的中点,求sin∠DAC.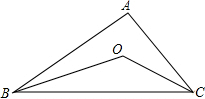 如图所示,BO,CO分别平分∠ABC和∠ACB.
如图所示,BO,CO分别平分∠ABC和∠ACB. 已知,如图,AB∥DC,AC、BD交于O,且AC=BD,求证:OD=OC.
已知,如图,AB∥DC,AC、BD交于O,且AC=BD,求证:OD=OC. 已知ABCD为正方形,E、F分别是AD、CD上的一点,∠EBF=45°,△EFD周长为2,求正方形边长.
已知ABCD为正方形,E、F分别是AD、CD上的一点,∠EBF=45°,△EFD周长为2,求正方形边长. 2013年开始,国家在113个环境保护重点城市和国家环境保护模仿城市开展PM2.5的检测工作并发布检测信息.“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物.某日随机抽取25个城市检测点的研究性数据,并绘制成统计表和扇形统计图如下:
2013年开始,国家在113个环境保护重点城市和国家环境保护模仿城市开展PM2.5的检测工作并发布检测信息.“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物.某日随机抽取25个城市检测点的研究性数据,并绘制成统计表和扇形统计图如下: