题目内容
6. 如图,二次函数y=ax2+bx+c图象的一部分,对称轴为x=$\frac{1}{2}$,且经过(2,0)这个点,有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
如图,二次函数y=ax2+bx+c图象的一部分,对称轴为x=$\frac{1}{2}$,且经过(2,0)这个点,有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )| A. | ①②③④ | B. | ③④ | C. | ①③④ | D. | ①② |
分析 根据抛物线的对称轴、开口方向以及与y轴的交点判断①;根据对称轴判断②;根据x=-1时,y=0判断③;根据抛物线的对称性判断④.
解答 解:①∵抛物线开口向下,
∴a<0,
∵抛物线与y轴交于正半轴,
∴c>0,
∵-$\frac{b}{2a}$=$\frac{1}{2}$,a<0,
∴b>0,
∴abc<0,正确;
②∵-$\frac{b}{2a}$=$\frac{1}{2}$,
∴-b=a,即a+b=0,正确;
③当x=-1时,y=0,
∴a-b+c>0,正确;
④根据抛物线的对称轴是x=$\frac{1}{2}$可知,点(0,y1)和点(1,y2)关于x=$\frac{1}{2}$对称,
∴y1=y2,正确,
故选:A.
点评 本题考查的是二次函数的图象与系数的关系,二次项系数a决定抛物线的开口方向和大小;一次项系数b和二次项系数a共同决定对称轴的位置;常数项c决定抛物线与y轴交点;b2-4ac的符号决定抛物线与x轴交点个数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.在△ABC中,∠B=90°,D是AC的中点,若∠A=20°,则∠BDC的度数为( )
| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
11.已知ab<0,则点P(a,b)在( )
| A. | 第一或第二象限内 | B. | 第二或第三象限内 | ||
| C. | 第一或第三象限内 | D. | 第二或第四象限内 |
15.某学生为了描点作出函数y=ax2+bx+c(a≠0)的图象,取了自变量的7个值,x1<x2<…<x7且x2-x1=x3-x2=…=x7-x6,分别算出对应的y的值,列出如表;
但由于粗心算出了其中一个y的值,请指出算错的是哪一个值?正确的值是多少?并说明理由.
| X | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| y | 51 | 107 | 185 | 285 | 407 | 549 | 717 |
16.将抛物线y1=-x2平移后得到y2=-x2+2x-2,则把抛物线y1平移到y2的方法是( )
| A. | 先向左平移1个单位,再向下平移1个单位 | |
| B. | 先向左平移1个单位,再向上平移1个单位 | |
| C. | 先向右平移1个单位,再向下平移1个单位 | |
| D. | 先向有平移1个单位,再向上平移1个单位 |
 已知抛物线y=ax2+bx+c的部分图象如图所示,若y<0,则x的取值范围是-1<x<3.
已知抛物线y=ax2+bx+c的部分图象如图所示,若y<0,则x的取值范围是-1<x<3. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a-2b+c>0;④a+c>0,其中正确结论的个数为( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a-2b+c>0;④a+c>0,其中正确结论的个数为( )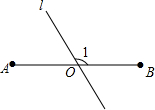 如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.
如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP=3或3$\sqrt{3}$或3$\sqrt{7}$.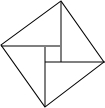 如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形的直角边分别为a、b,则ab的值是( )
如图,由4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形面积是17,小正方形面积是5,直角三角形的直角边分别为a、b,则ab的值是( )