题目内容
15.某学生为了描点作出函数y=ax2+bx+c(a≠0)的图象,取了自变量的7个值,x1<x2<…<x7且x2-x1=x3-x2=…=x7-x6,分别算出对应的y的值,列出如表;| X | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| y | 51 | 107 | 185 | 285 | 407 | 549 | 717 |
分析 根据表格可以得到相邻的y值的差,然后再将差值作差可以发现第几个y值是错的,从而可以算出正确的y值.
解答 解;x6对应的y值错误,正确的值是551,
理由是:通过表格可知,107-51=56,
185-107=78,
285-185=100,
407-285=122,
549-407=142,
717-549=168,
而78-56=22,100-78=22,122-100=22,142-122=20,
故x6对应的y值错误,正确的结果为:407+122+22=551.
点评 本题考查二次函数的图象,解题的关键是明确题意,发现其中的规律.

练习册系列答案
相关题目
5.已知在Rt△ABC中,∠C=90°,AC=2,BC=3,则AB的长为( )
| A. | 4 | B. | $\sqrt{5}$ | C. | $\sqrt{13}$ | D. | 5 |
6. 如图,二次函数y=ax2+bx+c图象的一部分,对称轴为x=$\frac{1}{2}$,且经过(2,0)这个点,有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
如图,二次函数y=ax2+bx+c图象的一部分,对称轴为x=$\frac{1}{2}$,且经过(2,0)这个点,有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
 如图,二次函数y=ax2+bx+c图象的一部分,对称轴为x=$\frac{1}{2}$,且经过(2,0)这个点,有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
如图,二次函数y=ax2+bx+c图象的一部分,对称轴为x=$\frac{1}{2}$,且经过(2,0)这个点,有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )| A. | ①②③④ | B. | ③④ | C. | ①③④ | D. | ①② |
10.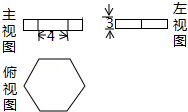 如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )
如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )
 如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )
如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )| A. | 24$\sqrt{3}$ | B. | 36$\sqrt{3}$ | C. | 72$\sqrt{3}$ | D. | 144$\sqrt{3}$ |
7.一次函数y=x+1的图象是( )
| A. | 线段 | B. | 抛物线 | C. | 直线 | D. | 双曲线 |
5.a、b都是实数,且a<b,则下列不等式的变形正确的是( )
| A. | ac<bc | B. | a+x>b+x | C. | -a>-b | D. | $\frac{a}{c}<\frac{b}{c}$ |
 如图所示,几何体是由4个相同的正方体组成的,它的左视图是( )
如图所示,几何体是由4个相同的正方体组成的,它的左视图是( )



 △ABC中,AB=5,AC=4,BC=6.
△ABC中,AB=5,AC=4,BC=6.