题目内容
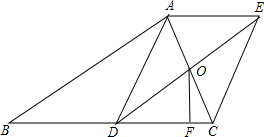 在Rt△ABC中,∠BAC=90°,且D是BC中点,过点A作AE∥DC,取AE=DC,连接CE.
在Rt△ABC中,∠BAC=90°,且D是BC中点,过点A作AE∥DC,取AE=DC,连接CE.(1)求证:四边形ADCE是平行四边形;
(2)求证:平行四边形ADCE是菱形;
(3)连接DE交AC于点O,过点O作OF⊥DC,若DF=8,AC=6,求OF.
考点:菱形的判定,平行四边形的判定
专题:
分析:(1)根据一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形;
(2)根据直角三角形斜边的中线等于斜边的一半可得AD=
BC,然后再证明AD=DC,根据邻边相等的平行四边形是菱形可得结论;
(3)首先利用勾股定理以及射影定理得出关于OF的关系式进而求出即可.
(2)根据直角三角形斜边的中线等于斜边的一半可得AD=
| 1 |
| 2 |
(3)首先利用勾股定理以及射影定理得出关于OF的关系式进而求出即可.
解答:(1)证明:∵AE∥DC,AE=DC,
∴四边形ADCE是平行四边形;
(2)证明:∵∠BAC=90°,且D是BC中点,
∴AD=
BC,CD=
BC,
∴AD=DC,
∵四边形ADCE是平行四边形,
∴平行四边形ADCE是菱形;
(3)解:设FC=x,FO=y,
∵平行四边形ADCE是菱形,
∴∠DOC=90°,
∵FO⊥DC,
∴可得:FO2=DF×FC,FO2+FC2=CO2,
∵DF=8,AC=6,∴CO=3,
即y2=8x,y2+x2=9,
解得;x=1,
故y=2
,
即OF的长为2
.
∴四边形ADCE是平行四边形;
(2)证明:∵∠BAC=90°,且D是BC中点,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=DC,
∵四边形ADCE是平行四边形,
∴平行四边形ADCE是菱形;
(3)解:设FC=x,FO=y,
∵平行四边形ADCE是菱形,
∴∠DOC=90°,
∵FO⊥DC,
∴可得:FO2=DF×FC,FO2+FC2=CO2,
∵DF=8,AC=6,∴CO=3,
即y2=8x,y2+x2=9,
解得;x=1,
故y=2
| 2 |
即OF的长为2
| 2 |
点评:此题主要考查了菱形、平行四边形的判定,以及直角三角形的性质,关键是掌握直角三角形斜边的中线等于斜边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将0.00002用科学记数法表示应为( )
| A、2×10-4 |
| B、2×10-5 |
| C、2×10-6 |
| D、0.2×10-4 |
若|x+y+2|+(xy-1)2=0,则(3x-xy+1)-(xy-3y-2)的值为( )
| A、3 | B、-3 | C、-5 | D、11 |
 如图,AE∥DC,∠A=∠C,BD平分∠ADC,则下列说法不正确的是( )
如图,AE∥DC,∠A=∠C,BD平分∠ADC,则下列说法不正确的是( )| A、AD∥BC |
| B、BC=DC |
| C、F为E中点 |
| D、AF=AD |
 如图,在平面直角坐标系中,已知A(3,4)、B(0,2),在x轴上有一动点C,当△ABC的周长最小时,C点的坐标为
如图,在平面直角坐标系中,已知A(3,4)、B(0,2),在x轴上有一动点C,当△ABC的周长最小时,C点的坐标为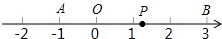 如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.
如图,点O是数轴的原点,且数轴上的点A和点B对应的数分别为-1和3,数轴上一动点P对应的数为x.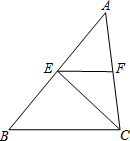 如图,在△ABC中,E、F分别是AB、AC的中点,△CEF的面积为2.5,则△ABC的面积为
如图,在△ABC中,E、F分别是AB、AC的中点,△CEF的面积为2.5,则△ABC的面积为
 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA+sinB=
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA+sinB=