题目内容
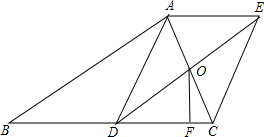
 如图,AE∥DC,∠A=∠C,BD平分∠ADC,则下列说法不正确的是( )
如图,AE∥DC,∠A=∠C,BD平分∠ADC,则下列说法不正确的是( )| A、AD∥BC |
| B、BC=DC |
| C、F为E中点 |
| D、AF=AD |
考点:平行线的判定与性质,等腰三角形的判定与性质
专题:
分析:首先证明∠A=∠AEB可得AD∥BC;再证明∠B=∠CDB,可得CB=DC,无法证明△AFD≌△EFB,故F为E中点,错误;然后再证明∠AFD=∠ADB,可得AF=AD.
解答:解:A、∵AE∥DC,
∴∠C=∠AEB,
∵∠A=∠C,
∴∠A=∠AEB,
∴AD∥BC,故A正确;
B、∵AD∥BC,
∴∠ADB=∠B,
∵BD平分∠ADC,
∴∠ADB=∠BDC,
∴∠B=∠CDB,
∴CB=DC,故B正确;
C、∵∠A=∠AEB,∠B=∠ADB,∠AFD=∠BFE,
没有边相等的条件,无法证明△AFD≌△EFB,
∴F为E中点,错误,故C错误;
D、∵AE∥DC,
∴∠BDC=∠AFD,
∵∠ADF=∠CDB,
∴∠AFD=∠ADB,
∴AF=AD,
故D正确;
故选:C.
∴∠C=∠AEB,
∵∠A=∠C,
∴∠A=∠AEB,
∴AD∥BC,故A正确;
B、∵AD∥BC,
∴∠ADB=∠B,
∵BD平分∠ADC,
∴∠ADB=∠BDC,
∴∠B=∠CDB,
∴CB=DC,故B正确;

C、∵∠A=∠AEB,∠B=∠ADB,∠AFD=∠BFE,
没有边相等的条件,无法证明△AFD≌△EFB,
∴F为E中点,错误,故C错误;
D、∵AE∥DC,
∴∠BDC=∠AFD,
∵∠ADF=∠CDB,
∴∠AFD=∠ADB,
∴AF=AD,
故D正确;
故选:C.
点评:此题主要考查了平行线的判定和性质,以及等角对等边,关键是掌握两直线平行,内错角相等,内错角相等,两直线平行.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 在Rt△ABC中,∠BAC=90°,且D是BC中点,过点A作AE∥DC,取AE=DC,连接CE.
在Rt△ABC中,∠BAC=90°,且D是BC中点,过点A作AE∥DC,取AE=DC,连接CE.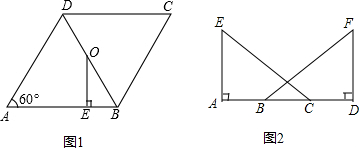
 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=4,则点P到AB的距离是
如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=4,则点P到AB的距离是 如图,矩形草坪长20米,宽10米,沿草坪三面有1米宽的小路,小路内外边缘所成的矩形相似吗?为什么?
如图,矩形草坪长20米,宽10米,沿草坪三面有1米宽的小路,小路内外边缘所成的矩形相似吗?为什么?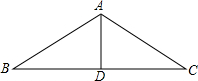 如图,厂房屋顶人字架(△ABC为等腰三角形),AB=AC的跨度BC为10米,∠B=26°,求中柱AD(D为底边BC的中点)和上弦AB的长.(精确到0.01米)
如图,厂房屋顶人字架(△ABC为等腰三角形),AB=AC的跨度BC为10米,∠B=26°,求中柱AD(D为底边BC的中点)和上弦AB的长.(精确到0.01米)