题目内容
 如图,在平面直角坐标系中,已知A(3,4)、B(0,2),在x轴上有一动点C,当△ABC的周长最小时,C点的坐标为
如图,在平面直角坐标系中,已知A(3,4)、B(0,2),在x轴上有一动点C,当△ABC的周长最小时,C点的坐标为考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:先作出点B关于x轴的对称点B′,连接AB′交x轴于点C,再用待定系数法求出过AB′两点的一次函数解析式,求出此函数与x轴的交点坐标即可.
解答: 解:先作出B关于x轴的对称点B′,连接AB′交x轴于点C,则B点坐标为(0,-2),
解:先作出B关于x轴的对称点B′,连接AB′交x轴于点C,则B点坐标为(0,-2),
由两点之间线段最短可知,AB′的长即为AC+BC的长,
因为AB是定值,
所以此时△ABC的周长最小,
设过AB′两点的一次函数解析式为y=kx+b(k≠0),则
,
解得k=2,b=-2,
故此一次函数的解析式为y=2x-2,
当y=0时,2x-2=0,解得x=1.
故C(1,0)时,△ABC的周长最短.
故答案为:(1,0).
 解:先作出B关于x轴的对称点B′,连接AB′交x轴于点C,则B点坐标为(0,-2),
解:先作出B关于x轴的对称点B′,连接AB′交x轴于点C,则B点坐标为(0,-2),由两点之间线段最短可知,AB′的长即为AC+BC的长,
因为AB是定值,
所以此时△ABC的周长最小,
设过AB′两点的一次函数解析式为y=kx+b(k≠0),则
|
解得k=2,b=-2,
故此一次函数的解析式为y=2x-2,
当y=0时,2x-2=0,解得x=1.
故C(1,0)时,△ABC的周长最短.
故答案为:(1,0).
点评:本题考查的是最短线路问题及用待定系数法求一次函数的解析式,能熟练运用一次函数的知识求出过AB′的函数解析式是解答此类问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
南平市是福建省九地市区域面积最大的地级市,它的面积约为26300平方千米,占全省的区域面积的
以上.将26300用科学记数法表示为( )平方千米.
| 1 |
| 6 |
| A、2.63×105 |
| B、2.63×104 |
| C、2.63×103 |
| D、26.3×103 |
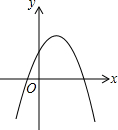 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a>0;②c>0;③b2-4ac>0,其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a>0;②c>0;③b2-4ac>0,其中正确的是( )| A、②③ | B、①② | C、①②③ | D、①③ |
 如图,已知直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD=3∠DOE,求∠AOF的度数.
如图,已知直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD=3∠DOE,求∠AOF的度数.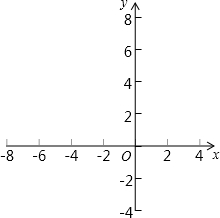 已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,OB=2,OC=8,抛物线的对称轴是直线x=-2.
已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,OB=2,OC=8,抛物线的对称轴是直线x=-2.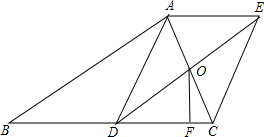 在Rt△ABC中,∠BAC=90°,且D是BC中点,过点A作AE∥DC,取AE=DC,连接CE.
在Rt△ABC中,∠BAC=90°,且D是BC中点,过点A作AE∥DC,取AE=DC,连接CE. 如图,矩形草坪长20米,宽10米,沿草坪三面有1米宽的小路,小路内外边缘所成的矩形相似吗?为什么?
如图,矩形草坪长20米,宽10米,沿草坪三面有1米宽的小路,小路内外边缘所成的矩形相似吗?为什么?